Motivation
- Feature-level augmentation방법은 변환과정을 직접적으로 처리하기 어려움
- Generative model based augmentation은 메모리랑 시간이 너무 많이듬
Method
- $\mathcal{E}$: feature extractor
- $\mathbf{z} \in \mathbb{R}^{d}$: feature embedding
- $K$ : 총 augmentation transforms의 숫자
- $T_{K}$: 총 augmentation transform
- $(T_{k}, \alpha_{k})$: transform과 하이퍼파라미터
- $\tau$: transform의 순차 적용함수. $\tau(x; (T_{k}, \alpha_{k})^{K}_{k=1})$
- $\rho$: $\tau$을 적용한것을 feature extractor을 통과한 경우와 근사시키는 모델
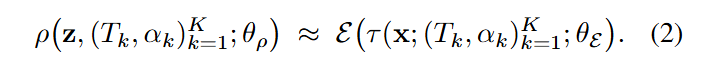
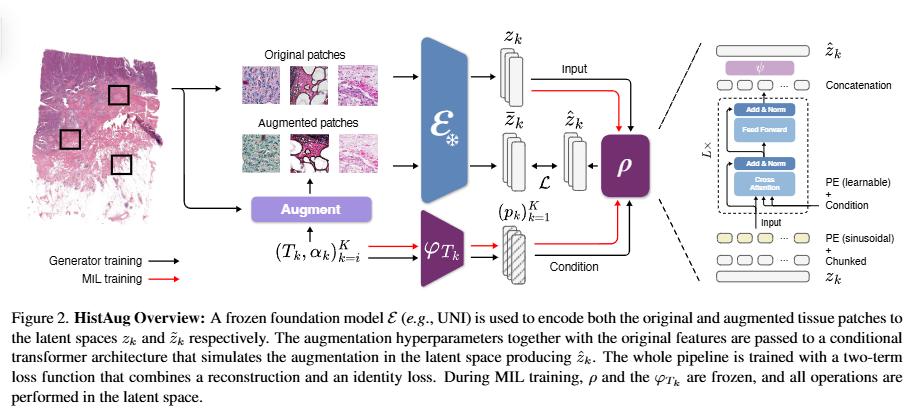
Generator
- $\mathbf{z} \mapsto (z_{i})^{C}$: 임베딩을 벡터를 C개로 나눔. 예) 1024차원에 C=4면 256짜리 4개의 벡터로만듬
- 변환과정마다 프로젝션 레이어를 둠. $\varphi_{T_{k}}$. 즉 변환과정종류마다 Linear layer을 두어야해서 여러 개 여야함.
- $\alpha_{k} \mapsto \mathbf{p}_{k} \in \mathbb{R}^{d/C}$: transformation($T$), 파라미터($\alpha$)을 Linear layer로 임베딩시킴.
- 학습가능한 포지션 임베딩 추가: $(\mathbf{p}_{k})_{k=1}^{K}$에 포지션 임베딩 더함.
- 셀프어텐션 + Residual connection: query(image), key/value (transformation token)

- Transformer layer을 통과하면서 나온 모든 임베딩을 concat한 후, MLP head을 통과시켜 최종임베딩을 구함.

- Loss function: 2가지 요소로 구성
- 직접적으로 변환+인코더와 증강결과의 차이가 없게 ($\rho(..) - \mathcal{E}$)
- 증강만함수만 인코딩하고, 실제변환을 안한(변환 파라미터을 이용, 예, flip=None) 것과 원본과 동
반응형
'Digital pathology' 카테고리의 다른 글
| 유전자 및 CD(Cluster of Differentiation) 정리 (0) | 2025.11.10 |
|---|---|
| ReMix: A General and EfficientFramework for Multiple InstanceLearning Based Whole Slide ImageClassification (0) | 2025.09.04 |
| PathGen-1.6M (2) | 2025.08.27 |
| Yottixel, SISH, RCCNet (3) | 2025.07.23 |
| Similar image search for histopathology: SMILY (1) | 2025.07.21 |



