이미지에서 blur(블러, 흐림 현상)을 확인하는 데 사용되는 다양한 알고리즘과 지표들이 있습니다. 주로 이미지의 선명도, 엣지(경계)의 강도를 측정하여 블러를 평가합니다.
이 평가하는 방법은 2가지가 있습니다.
- 원본과 대비가 가능한 경우: With reference image
- 원본과 대비가 필요 없는 경우: without reference image
이 포스팅에서 without reference image(no refereince image)인 대표적인 지표 및 알고리즘들을 크게 분류하면 다음과 같습니다.
- Spatial domain: 방법은 이미지의 픽셀과 인접 픽셀 간의 관계를 계산하여 흐림과 선명한 이미지를 구분하는 기법입니다.
- Grayscale Gradient base method: 이미지를 그레이스케일로 변환하여, 인접픽셀과의 그레디언트값(변화도)를 측정합니다. 측정된 변화도가 클수록 또렷한 이미지로 간주됩니다. 대표적으로 Laplacian variance가 있습니다.
- Spectral-domain: 이미지의 고주파 성분과 저주파 성분을 분석하여 이미지의 선명도를 평가하는 방법입니다. 고주파 성분은 이미지의 선명한 부분과 관련이 있으며, 세부 정보와 경계 정보를 많이 포함하고 있습니다. 반면 저주파 성분은 흐릿한 부분에 해당합니다
- Learning: 머신러닝을 이용한 방법
- Combination: 2개 이상의 조합을 이용하는 방법
1. Laplacian Variance (라플라시안 분산)
라플라시안 분산은 라플라시안 커널을 이용해서, 이미지의 2차미분을 구해 분산을 구하는 방법입니다. 이 분산이 뜻하는 바는 픽셀의 흩어짐 정도로, 또렷한 이미지일수록 높은 분산값을 가지며, 흐릿한 이미지일수록 낮은 분산값을 가지게 됩니다. 특정한 임계점을 두어 또렷하다, 흐리다라고 판단할 수 있습니다.
다음의 장점을 지닙니다.
- 간단하고 빠릅니다.: 계산이 비교적 간단하여 실시간 블러 감지에도 적합합니다.
- 효과적임: 엣지 정보를 기반으로 하므로 다양한 종류의 블러를 효과적으로 감지할 수 있습니다.
- 수학적 직관성: 분산을 이용한 접근 방식은 통계적으로도 타당성이 있습니다.
2차원 이미지에서는 다음과 같이 표현합니다. 2차미분을 구하기 위해서는 Laplacian kernel을 이용해서 구합니다.
$\nabla^2 I = \frac{\partial^2 I}{\partial x^2} + \frac{\partial^2 I}{\partial y^2}$
이를 메트릭스 연산으로 표현하면, 라플라시안 커널이 됩니다.
$$\begin{bmatrix}
0 & 1 & 0 \\
1 & -4 & 1 \\
0 & 1 & 0
\end{bmatrix}
$$
import cv2
import numpy as np
def cal_laplacian_variance(image_array: np.ndarray):
"""라플라시안 분산을 구함
Args:
image_array (np.ndarray): RGB image array
Returns:
float: Laplacian variance
"""
gray_image = cv2.cvtColor(image_array, cv2.COLOR_RGB2GRAY)
laplacian = cv2.Laplacian(gray_image, cv2.CV_64F)
return laplacian.var()라플라시안 분산은 분산이기에 항상 0또는 양의값을 갖게됩니다. 이런 경계면이 모호한 이미지를 바로 식별할 수 있습니다.

또는 경계면이 또렷한(=focal plane)에 맞게 하는 경우의 이미지도 선택할 수 있습니다.

2. Wavelet-based transform
이미지도 신호기이 때문에, 이를 신호로 처리하는 방법이 있습니다. Spectral-domain에 속하는 방법으로, 이미지를 저주파 및 고주파로 나눕니다. 각각 저주파 고주파는 다시, 저저, 고고, 저고,고저로 나눌 수 있고, 저저를 제외한 나머지 신호 강도를 이용하여 이미지의 선명도를 추출할 수 있습니다.
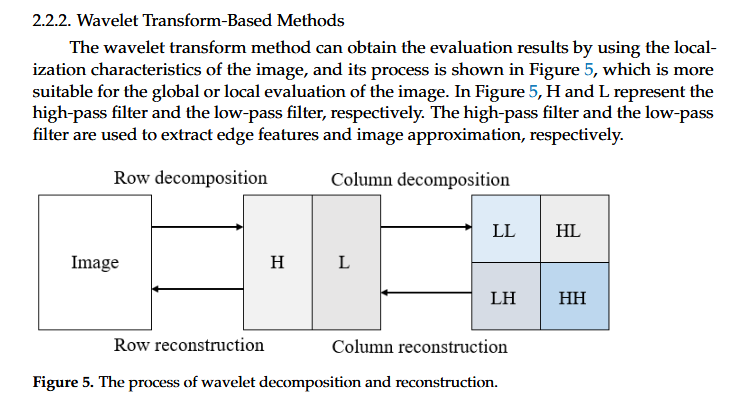
Blur Detection for Digital Images Using Wavelet Transform*이 논문에서도 저저주파를 제외하고 신호강도를 측정합니다.
def cal_wavelet(image_array):
# 이미지를 그레이스케일로 변환 (이미지가 컬러일 경우)
if len(image_array.shape) == 3:
image = cv2.cvtColor(image_array, cv2.COLOR_RGB2GRAY)
# 2D 웨이브렛 변환 수행 (Haar 웨이브렛 사용)
coeffs = pywt.dwt2(image, "haar") # 'haar' 외에도 다양한 웨이브렛 사용 가능
LL, (LH, HL, HH) = coeffs
# 고주파 성분 (LH, HL, HH)의 에너지를 합산하여 선명도 측정
high_freq_energy = (
np.sum(np.abs(LH) ** 2) + np.sum(np.abs(HL) ** 2) + np.sum(np.abs(HH) ** 2)
)
return high_freq_energy'Data science > Computer Vision' 카테고리의 다른 글
| DCL-GAN (Dual Contrastive Loss and Attention for GANs) (0) | 2025.04.07 |
|---|---|
| 극좌표계(Polar coordinates) 및 픽셀유동화 (0) | 2024.08.20 |
| [5분 컷 리뷰] Matthew's correlation coefficient loss (0) | 2024.07.25 |
| Segmentation loss (손실함수) 총정리 (3) | 2024.07.22 |
| [5분 컷 이해] DICE score의 미분 (0) | 2024.07.17 |


