요약
DICE loss에서 반영하지 못하는 background의 오분류를 패널티로 반영하기위한 손실함수. Confusion matrix의 요소들을 직접 사용하여 손실함수를 만듬.
DICE vs MCC(Mattew's correlation coefficient, MCC)
DICE loss을 사용하든, IoU(Jaccard loss)을 사용하든 둘 다 TN(True negative)에 대한 정보가 없습니다.
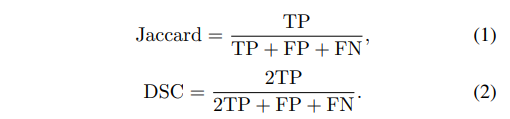
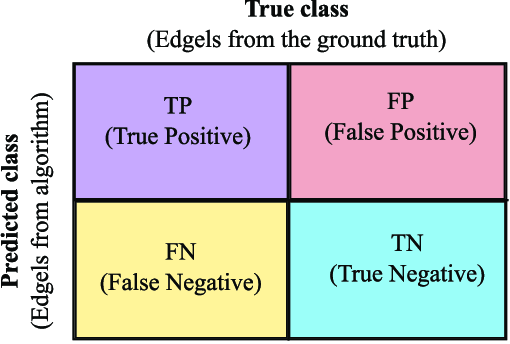
이 True Negative을 반영하기위해서, confusion matrix에서 각 요소를 아래와 같이 만듭니다. 즉, TP와 TN은 많이 맞추고, FP,FN은 적은 confusion matrix을 만들기를 바라며, 이를 정규화하기위한 분모로 만듭니다. 아래를 보면 각 요소들이 분모에 2번씩 사용됩니다.

MCC은 미분가능한가?
다행히 MCC은 segmentation에서 pixel wise로 연산하기때문에 미분가능합니다. 각 요소를 아래와 같이 표현 할 수 있기 때문입니다.
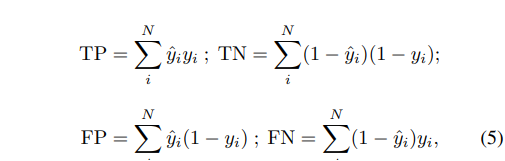
아래와 같이 1-MCC로 손실함수로 사용하고, 각 항목을 y예측값에 대해서 미분하면됩니다.

이 식을 pytorch로 구현하면 아래와 같습니다.
class MCCLosswithLogits(torch.nn.Module):
"""
Calculates the proposed Matthews Correlation Coefficient-based loss.
Args:
inputs (torch.Tensor): 1-hot encoded predictions
targets (torch.Tensor): 1-hot encoded ground truth
Reference:
https://github.com/kakumarabhishek/MCC-Loss/blob/main/loss.py
"""
def __init__(self):
super(MCCLosswithLogits, self).__init__()
def forward(self, logits, targets):
"""
Note:
위의 모든 코드가 logits값을 입력값으로 받고 있어서, logtis->confidence [0,1]으로 변경
MCC = (TP.TN - FP.FN) / sqrt((TP+FP) . (TP+FN) . (TN+FP) . (TN+FN))
where TP, TN, FP, and FN are elements in the confusion matrix.
"""
pred = torch.sigmoid(logits)
tp = torch.sum(torch.mul(pred, targets))
tn = torch.sum(torch.mul((1 - pred), (1 - targets)))
fp = torch.sum(torch.mul(pred, (1 - targets)))
fn = torch.sum(torch.mul((1 - pred), targets))
numerator = torch.mul(tp, tn) - torch.mul(fp, fn)
denominator = torch.sqrt(
torch.add(tp, 1, fp)
* torch.add(tp, 1, fn)
* torch.add(tn, 1, fp)
* torch.add(tn, 1, fn)
)
# Adding 1 to the denominator to avoid divide-by-zero errors.
mcc = torch.div(numerator.sum(), denominator.sum() + 1.0)
return 1 - mcc반응형
'Data science > Computer Vision' 카테고리의 다른 글
| 이미지 흐림 측정 방법 (2) | 2024.10.14 |
|---|---|
| 극좌표계(Polar coordinates) 및 픽셀유동화 (0) | 2024.08.20 |
| Segmentation loss (손실함수) 총정리 (3) | 2024.07.22 |
| [5분 컷 이해] DICE score의 미분 (0) | 2024.07.17 |
| [5분 컷 이해] Rotation matrix(회전 메트릭스) 구하기, 유도 (0) | 2024.03.18 |

