[5분 컷 리뷰] MiT(Mixed Vision Transformer). SegFormer: Simple and Efficient Design for SemanticSegmentation with Transformers

 

Motivation

1. 최근 연구들은 언어모델을 차용하여 비전문제를 풀려는 아키텍처가 많이 발표되고 있으며, 대표적으로 ViT(Vision Transformer)가 있습니다.
2. (2021년 당시) Vision Transformer을 기반으로한 모델들은 ViT을 인코더 백본으로 특징을 뽑고, CNN을 여러겹 적용하여 decoders로 하여 꽤 좋은 성능을 보여주었습니다.
3. 위의 아키텍처는 아래의 2문제가 있어, Segformer가 해결하고자 했던 것 입니다.
   1. Single scale low-resolution: 하나의 스케일의 feature만 사용된다는 것입니다. 인코더에서 이미지를 특징화하고, 디코더에서 하나의 입력스케일만 입력받습니다.
   2. Computational cost: 이미지가 클수록 계산량이 많다는 것입니다. 특히, 트랜스포머는 token 수 N의 N(O^{2})의 연산을 갖기에, 이미지 사이즈가 크면 연산량이 너무 많이 듭니다.

 

Segformer 장점

• Positional encoding(PE) 사용하지 않습니다. PE을 안쓰고, Zero padding과 CNN으로 위치정보를 포함시켰기 때문입니다. 덕분에, 여러 크기의 입력이미지를 수용할 수 있습니다. 
• 계층적 구조: Transformer에 들어가는 입력을 점진적으로 작게 나눠, 앞단에는 큰(거친, coarse)특징들 (예, 위치정보)를 뽑고, 후미의 블록에서는 상세한 특징(Fine)을 뽑도록 아키텍처가 구성되었습니다.
• 경량 All-MLP 디코더: 디코더에 CNN하나없이 MLP로만 구성되어, 더 큰 수용장(Effective Receptive Field)을 가집니다. 따라서, 이미지 분절시에 멀리 떨어진 픽셀정보를 고려할 수 있습니다.

 

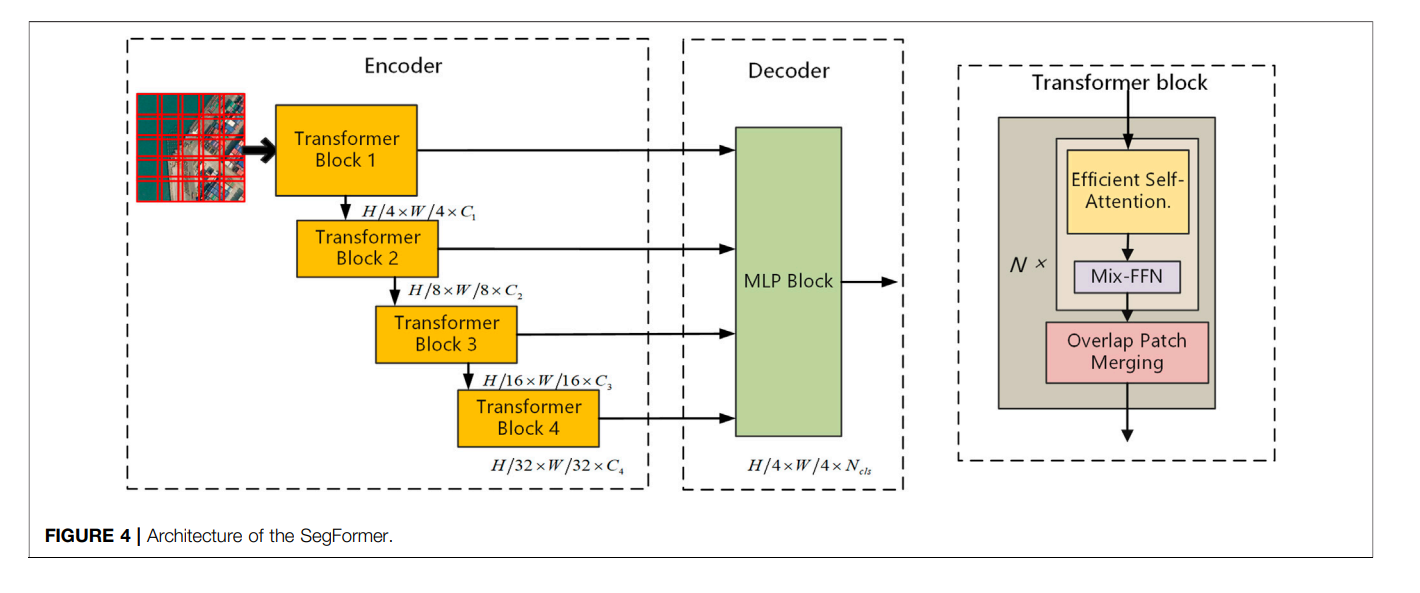
아키텍처 구성

Segformer은 크게 2가지의 구성입니다. 거의 모든 Segmentation 아키텍처와 동일하게 인코더와 디코더 구조를 갖습니다.

1) 인코더(Encoder): 계층적 트랜스포머(Hierachial Transformer). 트렌스포머의 패치크기를 다양하여 입력받습니다.

2) 디코더(All-MLP decoder) : 1)의 다양한 level의 features을 입력으로하는 디코더로, 최종적으로 $\frac{H}{4} \times \frac{W}{4} \times N_{cls}$의 이미지를 반환합니다. 이미지가 4배 작아져 다운샘플링 됩니다.

인코더의 메트릭스 크기는 입력피쳐(패치당) 사이즈입니다.

 

 

---

상세한 구성은 아래와 같습니다.

 

1. 입력 이미지: $H \times W \times 3$

2.계층패치화: 이미지를 $\frac{H}{2^{i+1}} \times \frac{W}{2^{i+1}} \times C_{i}$으로 패치화합니다. 예를 들어, 첫번째 트렌스포머 블럭에서는 패치(토큰)하나당 256/4 x 256/4 x C, 이후에는  256/8 x 256/8 x C2 이런식입니다.

3.패치 결합(Overlapped Patch Merge):

• 결합인데, 사실은 패치를 결합된 상태에서 분리한다는 것이 더 이해가 쉽습니다. $ N \times N \times 3$ 패치를 $ 1 \times 1 \times C $벡터로 표현이 가능합니다. 일단 백터화해놓으면, 이후의 인코더블럭들에서는 $ 1 \times 1 \times C_{i} $ 이든, $ 1 \times 1 \times C_{i+1} $이든 표현이 가능합니다. 일단 벡터화를 하면 아래와 같이 패치를 쪼갤 수 있습니다.
• 예를 들어,  첫 번째 입력이미지를 4x4로 쪼갠경우, 한 패치당 $\frac{224}{4} \times \frac{224}{4} \times C_{1}$ 크기를 갖습니다. 이 입력크기를 F1이라고 합니다. 이 F1을 입력크기를 다시 더 작은 단위의 크기로 쪼개서($ \frac{224}{8} \times \frac{224}{8} \times C_{2} $) 트랜스포머의 입력에 넣습니다. 트렌스포머 블럭1번째에서 1개 패치가 2번째트렌스포머 블럭의 4개가 되는것입니다.
• 이런 패치과정을 겹치지않게(non overlapping)하게 하면 패치간의 연속성이 떨어져서, 겹쳐가면서 진행합니다.  (사실 정확히 4개가 아닐 수 있습니다)

4. Efficient Self-Attention

어텐션은 패치 수(토큰 수)에 영향을 받습니다. 정확히는 패치수(N)의 제곱입니다. Segformer을 이 N을 R비율 맞큼 줄입니다.

N=W x H 라고 할 때,

1. $\text{ Reshape }(\frac{N}{R}, C \cdot R)$: 연산할 이미지의 수를 R배만큼 줄이고, 특징값을 R배만큼 늘립니다.
2. $Linear(C\cdot R, C)$: R배만큼 늘어난 이미지 특징값을 C로 다시 선형변환해서, 압축합니다.

이러면 원래 $O(N^{2})$ 이던 계산량이 $O(\frac{N^{2}}{R})$으로 변경됩니다.

5. Mix-FFN: CNN과 Feed-forward network(FFN)을 단계적으로 진행하는 모듈입니다.이미지 분할(Segmentation)에서는 사실 포지셔널 임베딩 필요없다고 저자들은 주장하는데요. 제로패딩만 어느정도해도 위치정보가 들어간다는 연구가 있기 때문입니다. 

$x_{out} = MLP(GELU(Conv_{3 \times 3}(MLP(x_{in}))) + x_{in}$

• $x_{in}$: self-attention 에서 나온 피쳐입니다.

6. All-MLP Decoder: CNN 보다 더 큰 수용장(Effective recept field, ERF)을 갖기위해서, 일부러 CNN을 사용하지 않고 MLP layer을 구차했습니다. 문제는 Transformer block에서 각기 다른 token(이미지)사이즈를 입력받아야하는데 아래와 같이 처리했습니다.

1. 채널 수 맞춤: $\hat {F_{i}} = Linear(C_{i}, C)(F_{i}), \forall i $. 모든 i(Transformer block의 output)에 대해서 채널을 C로 맞춥니다. 이렇게하려면 MLP가 4개가 있어야겠죠.
2. 업샘플링(upsampling): 모든 피처맵(F_{i})을 $\frac{H}{4} \times \frac{W}{4} $ 크기로 업샘플링을 합니다. 업샘플링은 Bilinear interpolation또는 Nearest interpolation로 해볼 수 있습니다.
3. 결합(Concatenate) 후 Linear: ${F = Linear(4C, C)(Concat( \hat {F_{i}})), \forall i $ 2.에서 나온 모든 피쳐맵을 한축으로 concat합니다. 그 이후 Linear 채널을 교정합니다.  
4. 분류: $M = Linear(C, N_{cls})(F)$ linear layer을 하나 넣어 클레스 수에 맞게 분류합니다.

 

아래 그림으로 보면 더 이해가 쉽습니다.

Yang, L., Wang, X., & Zhai, J. (2022). Waterline extraction for artificial coast with vision transformers.  Frontiers in Environmental Science ,  10 , 799250.

 

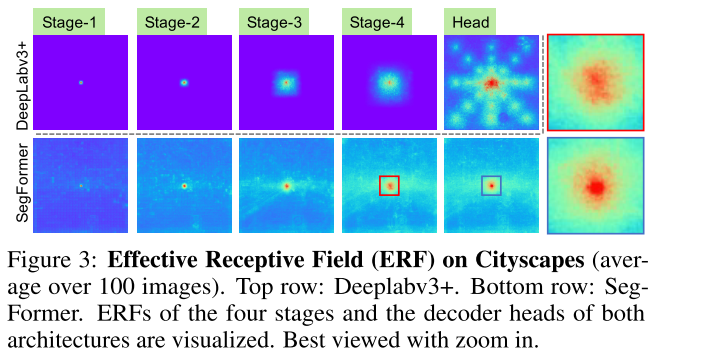
결과 1: 수용장이 더 커진게 맞나?

네, 수용장이 커졌습니다.

아래는 Cityscapes데이터셋에서의 100개이상의 이미지의 예측에서의 수용장을 시각화 한 것입니다. 실제로는 output값을 역전파해서 어떤 픽셀이 gradient가 컸는지 계산했을 것입니다. (https://ahmdtaha.medium.com/understanding-the-effective-receptive-field-in-deep-convolutional-neural-networks-b2642297927e)

DeepLabv3+ 모델과 SegFormer을 비교해봤을 떄, 더 큰 수용장을 보입니다. 특히, stage 4에서는 DeepLabV3+가 중심부에만 몰려있습니다.

 

모델사이즈에 따른 성능은?

인코더와 디코더 사이즈를 키울수록 mIoU지표는 확실히 좋아집니다.

 

PE 대신에 Mix-FFN(CNN+MLP)을 쓴게 더 좋은가?

포지셔널인코딩은 이미지 사이즈가 커지면, 포지셔널 인코딩을 Interpolation해서 사용해야하는데, 이 Interpolation때문에 성능열하가 존재한다고 이미 알려져있고, 그 결과도 재현되었습니다. PE로는 성능차이가 크게 떨어반해, Mix-FFN으로는 성능 열하가 적게 보여집니다.

 

Discussion

Segformer는 positional encoding 없이도 다양한 입력 이미지 크기를 처리할 수 있는 유연성을 가지며, 계층적 구조와 효율적인 self-attention 메커니즘을 통해 계산 효율성을 극대화합니다. 또한, 경량의 All-MLP 디코더를 채택하여 더 큰 수용장을 확보함으로써, 이미지 분할과 같은 작업에서 더욱 정교한 결과를 보였습니다.