요약
iBOT(masked image modeling)과 DINO(knowledge distillation with no label)방법을 혼합한 방법
Transactions on Machine Learning Research (01/2024)
Data processing: LVD-142M dataset의 생성과정
많은 양의 데이터 학습을 위해, 데이터 처리방식을 1) 라벨, 비라벨 이미지 수집, 2) 중복이미지 제거, 3) 이미지 검색
- 데이터 수집: 데이터 수집은 라벨링된 데이터와 라벨링 안된 데이터 크게 2가지의 데이터셋을 구축했습니다. 라벨링 된 데이터는 classifcation, segmentation, depth estimation 등의 다양한 문제에 사용되는 공공데이터를 수집했습니다. 다른 한편으로는 웹크롤링을 통해서 <img>테그가 있는 경우를 모두 가져오고, PCA hash dedupliation 등을 이용해서 이미지의 중복을 제거했습니다.
- 중복제거(de-duplication): 비슷한이미지만 모여있으면, 이미지의 다양성을 학습하기 어려우니, 유사한 이미지들을 제거하기위해서 중복제거를 image-copy-detection알고리즘을 이용해서 처리했습니다.
- Self-supervised image retrieval: 라벨링된 데이터셋과 라벨링안된 데이터셋에서도 매우 비슷한 이미지가 있을 수 있기때문에, 이를 제거해야합니다. 첫 번째로, 이미지를 사전학습된 ViT-H/16로 "비정제 /정제 "임베딩 시키고 각 이미지를 코사인유사도로 유사성을 평가합니다. 그 후, K-means clustering을 이용해서 "비정제" 데이터를 군집화합니다. 하나의 정제 이미지의 벡터를 이용해서, 가장 가까운 N(4)의 이미지를 검색합니다. 1개의 정제데이터에 대해서, 비정제 데이터 4개의 유사한 Cosine similarity을 확인하고, 유사도가 낮으면(=이미지가 충분하지 않다면), 쿼리 이미지가 속한 클러스터에서 추가로 M개를 샘플링해서 보완합니다.
실제 구현은 vector DB로 쓰이는 Faiss 을이용해서 진행했습니다. 약 20개의 노드에서 위 과정을 분산처리하여 LVD-142M dataset을 생성합니다.
Discriminative Self-supervised Pre-training
이 연구에서 제안하는 방법론은 DINO와 iBOT loss을 혼합하는 방법론입니다. 이를 혼합하기 위해서, Student모델과 Teacher model은 각각 2개의 head을 가지고 있게됩니다.
1. Image-level objective: DINO v1에서 사용했던 것과 같습니다. Student, Teacher 모델이 있고, Student model이 반환하는 vector 와 teacher model이 반환하는 vector가 유사해지는 것을 목적으로합니다. (+centering + moving average에 대한 설명). 그 후, 파라미터는 EMA(Exponential moving average)로 student model에서 teacher 모델로 반영합니다.
$L_{DINO}=-\sum p_{t}log p_{s}$
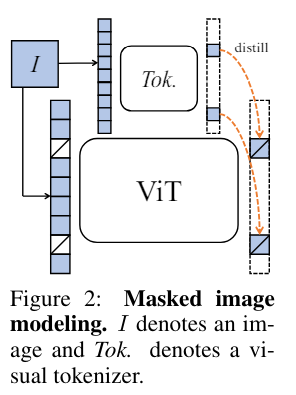
2.Patch-level objective: iBOT을 이용한 자기지도 학습입니다. iBOT은 MIM(Masked image modeling0)으로 이미지를 더작은 패치로 나눈다음에 훈련하는 방법을 의미합니다. 이렇게 만든 저 작은 패치를 랜덤으로 마스킹합니다. (Fig 2. iBOT) 마스킹된 경우 마스킹 토큰만 줍니다.
- $\textbf{x}=\{x_{i}\}^{N}_{i=1}$: 이미지를 작은 토큰으로 생각해서, 패치단위로 N개로 잘게 쪼갭니다.
- $\textbf {m}^{N}$: 마스킹인덱스입니다. 0 또는 1입니다. N개의 패치마다 마스킹할건지 여부를 결정합니다. $m_{i}=1$이면 마스킹된 상태입니다.
- $\tilde{x}\triangleq \{\textbf {x}_{i} | m_{i}=1\}$: 마스크된 이미지를 의미합니다. m=1인 경우, 이미지들이 마스크 토큰으로 변경됩니다.
- $\hat{x}\triangleq \{\tilde{x}|(1-m_{i})x_{i} +m_{i}\textbf {e}_{[MASK]}\}$: N개의 패치가 마스크 토큰 또는 보존
학습의 목적은 마스크된 토큰($\tilde{x}$)을 복원하는 학습을 합니다. 아래의 그림 Figure 2에서, VIT(student)에는 마스크된 토큰을, teacher 모델에서는 전체의 패치를 다 본 후, masking 된 패치만 가져와 두 분포가 동일하도록 하는 것을 원합니다.
$L_{MIM} = -\sum _{i=1}^{N}m_{i}\cdot P_{\theta}^{patch}(u_{i})^{T} log P_{{\theta}}^{patch}(\hat{u_{i}})$
위 식에서 $m_{i}$가 곱해져서 반드시 마스킹된 경우만, 임베딩값을 복원하는 문제로 변경됩니다. 여기서도 DINO와 마찬가지로 softmax, centering이 쓰입니다. 논문에서는 아래와 같이 간략하게 표현했습니다.
$L_{iBOT}=\sum_{i} p_{ti}logp_{si}$ (i:masked patch index, t: teacher model, s: student model)
3. 두 해드의 파라미터는 공유: Zhou et al(2022)에 논문에선서는 DINO와 iBOT의 해드 파라미터를 공유하는게 더 나은 성능을 보였으나, 본인들이 실험해보니 따로두는게 더 나았다고합니다.
4. Sinkhorn-Knopp centering: DINO에서는 teacher모델의 표현을 centering 후의 temperature scaling을 진행합니다. DINO v2에서는 SK(Sinkhorn-Knopp) batch normalization을 사용하는게 더 낫다고하여 Sinkhorn-knopp algorithm을 진행합니다.
5. KoLeo regularizer: 배치내에서 피쳐가 균등하게 만들기위해서 KoLeo regularizer을 사용합니다. KoLeo 정규화전에 각 벡터에 L2 norm을 진행합니다.
$L_{koleo}= -\frac{1}{n}\sum_{i=1}^{n}log(d_{n,i})$,
$d_{n,i}=min_{j=i}||x_{i}-x{j}||$은 벡터i와 배치 내에 어떤 벡터든간의 최소거리를 의미합니다. 벡터를 L2 norm을 진행하면 거리가 1로 정규화되고, 각만 달라지게됩니다. 이 벡터들간의 거리가 좁을 때, 점점더 좁아지면 -log값이 매우커지니 서로 띄어놓게하기위해(uniform span) 이 정규화를 진행합니다.

6. Adapting the resolution: 작은 이미지를 패치로 나누면 더 작게되어 pixel level task(semgnetaion, detection)등에서 성능열하가 발생합니다. 그렇기에 학습후반에만 일부 큰 이미지518x518로 학습합니다.
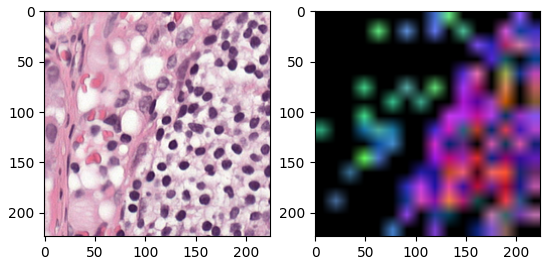
DINO v2의 PCA시각화
비지도학습을 이용해서, 임베딩값이 어떻게 픽셀상에 표현되는지 알기위해, 각 이미지를 RGB로 3개의 주성분을 가진 경우로 표현합니다. 임베딩을 주성분(각 성분은 RGB로 취급)하여 시각화합니다. 이 단계는 4단계로 구분됩니다.
- 첫 번째 PCA 수행:
- 모델을 사용하여 이미지 패치(조각)들을 추출하고 이를 통해 특성(features)을 얻습니다.
- 이 특성들에 대해 첫 번째 PCA를 수행하여 주성분들을 구합니다.
- 첫 번째 주성분(첫 번째 컴포넌트)을 기준으로, 값을 임계값(threshold) 이상인 패치들만 남깁니다. 이렇게 하면 이미지의 주요 객체와 배경이 분리됩니다. 이 과정에서 첫 번째 주성분 방향이 가장 큰 분산을 설명하기 때문에, 주성분 값을 기준으로 분리하면 주로 배경과 전경이 나눠집니다.
- 배경과 전경 분리:
- 첫 번째 주성분 값을 기준으로 배경과 전경이 분리된 후, 배경 패치를 제외한 나머지 패치들만 남깁니다. 즉, 전경 패치들만 남기게 됩니다.
- 두 번째 PCA 수행:
- 전경 패치들에 대해 두 번째 PCA를 수행합니다. 여기서 주성분 3개를 추출합니다.
- 이 주성분들은 이미지의 주요 객체의 다양한 부분들을 설명하는 데 사용됩니다.
- 시각화:
- 두 번째 PCA로 얻은 3개의 주성분을 각각 R, G, B 채널에 할당하여 시각화합니다. 이렇게 하면, 이미지의 주요 객체의 다른 부분들이 서로 다른 색상으로 표현됩니다.
아래의 이미지를 샘플로 진행해보겠습니다.
from torchvision.io.image import read_image
from torchvision.transforms import ToPILImage
from matplotlib import pyplot as plt
image = read_image("....png")
plt.imshow(ToPILImage()(image))
dino 모델의 입력스케일이 [0, 1]의 float이기 때문에 /255로 나누고 `forward_features`메서드로 포워딩해줍니다. features은 dictionary 형태로 나오고, cls token을 포함한 여러가지 output이 나옵니다. 이 중에서, 패치단위로 나눈 토큰(token)의 벡터를 구하기 위해서 "x_norm_patchtoken"의 값을 가져옵니다.
embedding_patch(E_patch)의 shape은 (1, 256, 178)인데, 1은 하나의 이미지, 256은 token의 수(패치수), 768은 임베딩 차원을 의미합니다.
import torch
from einops import rearrange
from torchvision.transforms import Normalize
from torchvision.transforms.functional import resize
IMAGENET_DEFAULT_MEAN = (0.485, 0.456, 0.406)
IMAGENET_DEFAULT_STD = (0.229, 0.224, 0.225)
norm = Normalize(mean=IMAGENET_DEFAULT_MEAN, std=IMAGENET_DEFAULT_STD)
I_norm = norm(image / 255)
dinov2 = torch.hub.load('facebookresearch/dinov2', 'dinov2_vitb14')
features = dinov2.forward_features(I_norm.unsqueeze(0))
E_patch = features["x_norm_patchtokens"]
print(E_patch.shape) # (1, 256, 768)
<class 'dict'> dict_keys(['x_norm_clstoken', 'x_norm_regtokens', 'x_norm_patchtokens', 'x_prenorm', 'masks'])
torch.Size([1, 256, 768])
PCA을 돌리기위해서 3차원의 1의 배치를 squeeze하여 2차원으로 변경해줍니다. (1, 256, 768) -> (256,768). 그리고, PCA로 주성분을 구하고, 그 주성분중에 가장 큰 주성분 벡터(V[:, 0])을 뽑아서, 임베딩 차원 -> 주성분차원으로 정사영(projection)시켜줍니다.
E_patch_norm = E_patch.squeeze(dim=0)
print(E_patch_norm.shape)
_, _, V = torch.pca_lowrank(E_patch_norm) # V은 주성분. 각 벡터는 직교(orthogonal)
E_pca_1 = torch.matmul(E_patch_norm, V[:, 0])주성분으로 프로젝션된 각 패치들 중에는 배경도 있고, 전경도 있을것입니다. 이 주성분은 가장 분산이 큰 설명하는 벡터이기에 배경/전경을 설명할 수 있습니다. 따라서, 주성분 1번(인덱스0번)에 내적하여 projection시킵니다.
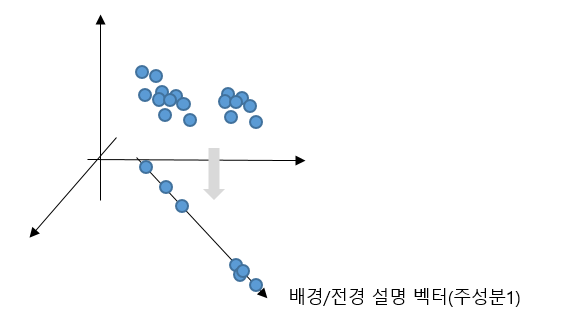
프로젝션된 벡터를 정규화하여, threshold을 걸어 배경과 전경을 분리합니다. 각 256 패치들이 전경에 속하는지, 배경에속하는지에 대한 마스킹을 갖계됩니다(boolean). 여기까지가 첫 번째 PCA이후, threshold을 걸어 배경과 전경을 분리하는 것입니다..
def minmax_norm(x):
"""Min-max normalization"""
return (x - x.min(0).values) / (x.max(0).values - x.min(0).values)
E_pca_1_norm = minmax_norm(E_pca_1)
print(E_pca_1_norm.shape)
M_fg = E_pca_1_norm.squeeze() > 0.5 # (256, )
M_bg = E_pca_1_norm.squeeze() <= 0.5 # (256, )
여기서, 전경의 픽셀만 다시 분리하여 PCA을 새롭게 진행합니다. 이 두 번째 PCA의 목적은 주성분을 3개를 뽑아서RGB에 대응시켜 모델이 어느 패치(포지션)을 보고 임베딩을 했는지, 의미있게 임베딩했는지 확인해보자는 것입니다. 마찬가지로, 전경만 뽑아 PCA을 합니다.
PCA의 결과는 (N, 3)입니다. N은 전경의 패치수, 3은 프로젝션된 값입니다.
# 전경 패치만 뽑아서, PCA을 돌립니다.
_, _, V = torch.pca_lowrank(E_patch_norm[M_fg])
# PCA에서 가장 분산이 큰 주성분 3개를 뽑아 각 벡터에 projection합니다.
E_pca_3_fg = torch.matmul(E_patch_norm[M_fg], V[:, :3])
E_pca_3_fg = minmax_norm(E_pca_3_fg) # (N, 3)
여기서 (N, 3)을 다시 이미지로 그려야합니다. (256,)의 패치에 전경부분만 (N, 3)의 (, 3)의 값들을 넣어줘야합니다. 그리고 각 패치에 맞도록 다시 rearange해줍니다. 이 과정은 (256, 3)을 패치 형태에 맞는 (16, 16, 3)으로 바꾸는 과정입니다.
B, L, _ = E_patch.shape
Z = B * L
print(Z)
I_draw = torch.zeros(Z,3)
I_draw[M_fg] = E_pca_3_fg
I_draw = rearrange(I_draw, "(B L) C -> B L C", B=B)
I_draw = rearrange(I_draw, "B (h w) C -> B h w C", h=224//14, w=224//14)
print(I_draw.shape)
R, G, B형태에 맞게 시각화하고 resize해줍니다. 아래의 우측그림과 같이 우 하단영역의 염증부분에 더 많이 강조가 됨을 알 수 있습니다. 반면 좌측상단은 stroma부분으로 이 부분을 주의깊게 설명하는건 아니라는 것으로 해석해볼 수 있습니다.
# Unpacking PCA images
image_1_pca = I_draw[0]
# To chanel first format torchvision format
image_1_pca = rearrange(image_1_pca, "H W C -> C H W")
H, W = 224, 224
# Resizing it to ease visualization
image_1_pca = resize(image_1_pca, (H,W))
from matplotlib import pyplot as plt
fig, axes = plt.subplots(1, 2)
axes[0].imshow(ToPILImage()(I))
axes[1].imshow(ToPILImage()(image_1_pca.detach()))