Introduction
NLP분야에서는 masked language라는 사전학습 전략으로 Transformer가 매우 인기를 끌었습니다. 반면, 비전테스크에서는 CNN의 대안으로 ViT가 쓰이는 것 같지만, 아직까지는 계산비용도 크고, 데이터도 많이필요해서 큰 이점을 못 얻고 있었습니다. 이 논문은 자기지도학습(Self-supervised learning)이라는 사전학습을 방법론을 이용해서, 비전테스크에서도 성공적인 사전학습을 할 수 있을지, 그리고 그 방법을 제시합니다.
언어문제에서는 self-supervised learning의 pretext task로 masked language 을 진행합니다. 반면, 이미지 분류문제에서는 풍부한 이미지의 정보(예, 형태, 컬러 등)이 이미지에 포함되어 있습니다. 그리고, 이 풍부한 이미지의 몇몇으로 특징을 잘 추출해서 N개의 분류를 하는 문제를 풀게됩니다. 풍부한 이미지에 오직 사전에 정의한 N개의 분류문제만 풀기에, 더 작은 특징만 추출하여 학습한 다는 것 입니다. 그렇기에, 더 많은 정보를 학습할 수 있다면, Vision 문제를 더 잘 이해할 수 있는 향상점(room)이 아직 있다고 생각합니다.
Methods: DINO (knowledge distillation with no label)
DINO을 이해하기 위한 주요 내용은 아래와 같습니다
- self-distiallation의 전체적인 구조(overview)
- objective function 및 data augmentation 방법 (SSL을 위한)
- Teacher network의 학습
1. Self-distillation의 전체적인 구조
DINO을 이해하기 위해서는 knowledge distillation에 대해서 먼저 이해해야합니다. 지식증류(knowledge distillation)의 이전 글(URL)을 보시면, 더 자세한 내용을 이해할 수 있습니다. 간략하게 지식증류를 요약하면, "큰 모델(teacher model)의 결과(output)은 큰 모델의 파라미터들의 정보들의 집약체이기에, 이 결과값(output)을 학습하는 작은 모델로 큰 모델을 성능/파라미터를 답습할 수 있다"라는 것입니다.
이 지식증류 방법중에 DINO은 teacher-student model에 해당됩니다.
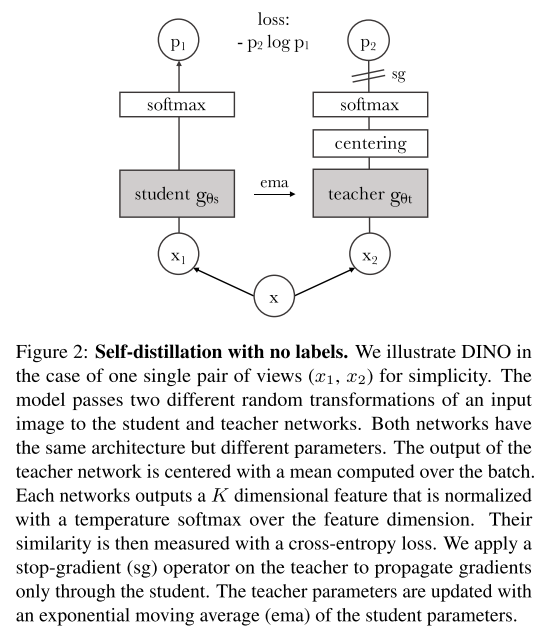
DINO을 가정은 2가지 모델이 있다고 가정합니다. 일반적인 student, teacehr모델은 크기가 다른 반면, DINO에서는 두 모델의 아키텍처는 동일합니다.
- teacher model($g_{\theta_{t}}$): 큰 모델을 의미하며, 이 모델의 파라미터는 $\theta_{t}$입니다.
- student model($g_{\theta_{s}}$): 작은 모델을 의미하며, 이 모델의 파라미터는 $\theta_{s}$입니다.
- input image($x$): 입력 이미지
- output probablity distribution ($P_{t}, P_{s}$): teacher model의 output($P_{t}$), student model의 output($P_{s}$) 입니다. 분포는 K개의 클레스의 분류라고 가정하여 K 차원의 크기입니다. 확률값처럼 해석하기위해서 softmax로 정규화한 값입니다. 좀 더 자세하게는 아래와 같이 표현할 수 있습니다. softmax함수의 입력값으로 전달하기전에 temperature scale을 주어, 분포의 뾰족한 정도(sharpness)을 조절할 수 있습니다. 분포를 평평하게 또는 클레스별로 차이가 심하게 나도록 조절한 후에 계산하는 값입니다. 아래의 식은 $P_{s}$인 student 모델의 확률분포값이고, t도 마찬가지로 그 아래의 식처럼 표현 가능합니다.
$P_{s}(x)^{(i)}=\frac{exp(g_{\theta_{s}}(x)^{(i)}/\tau_{s})}{\sum_{k=1}^{K}exp(g_{\theta_{s}}(x)^{(i)}/\tau_{s})}$
$P_{t}(x)^{(i)}=\frac{exp(g_{\theta_{t}}(x)^{(i)}/\tau_{t})}{\sum_{k=1}^{K}exp(g_{\theta_{t}}(x)^{(i)}/\tau_{t})}$
DINO은 teacher network($g_{\theta_{t}}$)은 주어진 것처럼 생각하여(no label에서 teacher model을 만들 수 없습니다. no label임에도 teacher model이 주어진것처럼 하는 이유는 아래에서 설명), teacher network의 결과분포와 student network의 결과 분포를 유사하게 만들도록합니다. 식으로는 아래와 같이 표현합니다. 즉, student 모델을 학습하도록 조절하는 것입니다.
$min_{\theta_{s}}H(P_{t}(x), P_{s}(x))$, where $H(a,b)=-alog(b)$ (2)
2. objective function 및 data augmentation 방법
DINO은 student모델은 국소적인 이미지만 학습하고, teacher 모델은 전역적인 이미지를 학습해서, 국소적인 이미지만 보더라도 전역을 예상할 수 있게끔 학습을 유도합니다. 좀 더 자세히는, DINO방법으로 자기 지도 학습시에는 이미지를 여러 방법에 따라 증강시키는데요(본문내에서는 view라고 표현). 이 증강의 방법을 2가지로 분류합니다. 한 이미지로 부터 아래의 증강된 이미지를 만듭니다(view)
- global views: $x_{1}^{g}, x_{2}^{g} $ -> teacher model에만 학습
- local views: 여러개의 더 작은 패치(smaller resolution) -> student model에만 학습
주의할 것은 global view라고 하나의 이미의 전체를 쓰는 것이 아니라, 일부 영역(50%이상)의 영역을 쓰는 것을 의미합니다. 반면 local view은 50%미만의 픽셀만 넣은 것입니다.
이를 "local-to-global" correspondences라고 합니다. 이에 대한 목적함수는 아래와 같습니다.
$min_{\theta_{s}}\sum_{x\in\{x_{1}^{g},x_{2}^{g}\}}\sum_{~x'\in V,~ x'!=x} H(P_{t}(x),P_{s}(x'))$ (3)
- $V$: 모든 증강된 이미지의 집합(global view + local view)을 의미합니다.
- $x'$: $V$의 원소인, 하나의 증강된 이미지를 의미합니다. 단 $ x'!=x $의 조건식이 있으니, global view은 아니어야합니다.
- $P_{t}(x)$: global view 이미지를 입력으로 받은 teacher 모델이 반환한 확률분포입니다.
- $P_{s}(x')$: local view 이미지를 입력으로 받은 student모델이 반환한 확률분포입니다.
- $min_{\theta_{s}}$: student모델의 파라미터를 최적화해서 global view을 입력으로한 결과를 유사하게 만듭니다.
3. Teacher network의 학습
지식증류를 하려면 결국에서는, 학습이 완료된 모델인 teacher model ($g_{\theta_{t}}$)가 있어야합니다. teacher model이 있을리 없죠. 그렇게 각 iteration을 진행하면서, 이전 iteration의 student model을 teacher model로 활용하려고합니다 (지식증류를 no label로 쓰기위한 기술적인 하이라이트입니다.). 이때, teacher model은 지수평활(exponential moving average, EMA)을 이용하여 다음과 같이 학습합니다.
$\theta_{t}\leftarrow \lambda \theta_{t} +(1-\lambda)\theta_{s}$, where $\lambda$ cosine schedule from 0.996 to 1
즉, student model parameter의 일부 영향과, teacher model의 parameters 일부을 조합하여 teacher model로 화용하겠다는 것입니다. 이걸 momentum encoder라고 하고 MoCO라는 contrastive learning 방법에서 사용되었던 방법입니다.
4. Avoiding collapse
추가로, 자기지도학습을 하는 모델들은 features collapse라는 모델의 특징값이 한쪽에만 쏠리거거나, 하나의값으로만 내뱉어져서, 다른 차원들의 값이 없는 경우가 발생하는데, centering과 sharpening(temperature scaling)을 이용하여 이를 해결할 수 있습니다. centering은 teacher model과 student model이 결과값이 균등분포로 나오는것막을 수 있습니다. 예를 들어, student model이 $p_{t}(x)$가 1.0이 한 벡터의 원소, 나머지는 0이라면 mode collapse가 발생할 수 있습니다. 내가 원하는 벡터의 차원이 N개인데, 1개의 벡터의 원소로만 변화가 지배되는 것입니다. 그렇기에 centering과 sharpening을 진행합니다.
- Centering은 배치의 효과를 조금 줄여, 다양한 차원으로 학습되게끔합니다. 단점은 균등분포로 나올수도 있습니다. centering할때의 중심값 (c)은 아래와 같이 계산합니다 (식 4). 이렇게 구한 c은 벡터형태로, 배치별 평균(First-order statistics)이며, 이전 배치별 평균값을 조합하여 사용합니다. teacher model의 결과값에 빼주게됩니다.
$c \leftarrow mc + (1-m)\frac{1}{B}\sum_{i=1}^{B}g_{\theta_{t}}(x_{i})$
- sharpening: 모델의 출력값의 분포가, 균등분포로 나오게 하는 것을 방지합니다. 즉, 한 차원에 학습이 될 수 있도록 합니다. 단점은 한 차원으로만 학습될 수도 있습니다 (centering과 반대)
pytorch 구현에서는 아래와 같습니다.
import torch
import torch.nn.functional as F
# teacher centering and sharpening
temp = self.teacher_temp_schedule[epoch] # 에폭별 temp저장
teacher_out = F.softmax((teacher_output - self.center) / temp, dim=-1) # Centering + sharpness
teacher_out = teacher_out.detach().chunk(2)



