요약
CNN을 이용한 영상분류에서는 사후해석으로 CAM, Grad-CAM등이 사용됩니다. 이 논문은 CAM방법론들에서 사용하는 Gradient을 이용하지 않고, Activation map에서의 가중치를 직접 획득하는 방식으로, 점수를 직접 산합니다.
Introduction: CAM-based explantation에서 사용하는 gradient을 해석에 충분한 방법이 못된다.
Score-CAM을 이해하기위해선 CAM부터 이해해야합니다. CAM은 GAP(Global average pooling)레이어가 꼭 포함되어야하는 방법론입니다 (Figure 1). Activation map(l-1번째 레이어) 이후에 GAP(l번쨰 레이어)가 들어가고 GAP 이후에 Fully connected layer(l+1번째 레이어)가 포함되어있습니다.
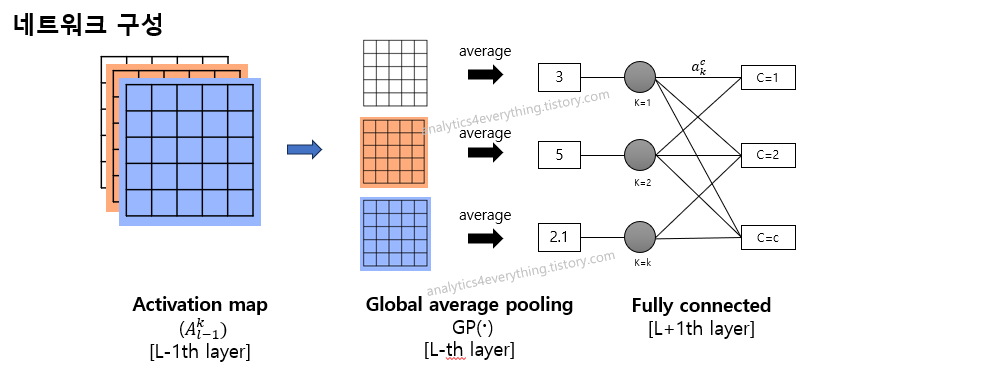
이때, CAM으로 1번 클레스의 가중치를 구하려면, Activation map(L-1번째 레이어)의 각 채널(k)에서 얻어진 feature map에 GAP 이후의 연결되는 가중치($a_{k}^{c=1}$)에 대해서 선형결합후에 ReLU만 씌우면 됩니다. 그래서, CAM은 아래와 같이 계산합니다.
$L^{c}_{CAM}=ReLU(\sum_{k}a_{k}^{c}A^{k}_{l-1})$

CAM은 각 activation map($A_{l}^{k}$)가 각각 채널별로 다른 공간정보를 담고 있다고 가정하여, 각 채널이 클레스에 미치는 가중치($a_{k}^{c}$)을 다시 선형결합해서 곱해줍니다. 하지만, CAM의 문제는 1) GAP layer가 없는 네트워크가 없는 경우에 사용할 수 없고, 2) fully connected layer가 없거나, 2개 이상인 경우에는 가중치($a_{k}^{c}$)을 구할 수 없기에 연산이 불가능합니다.
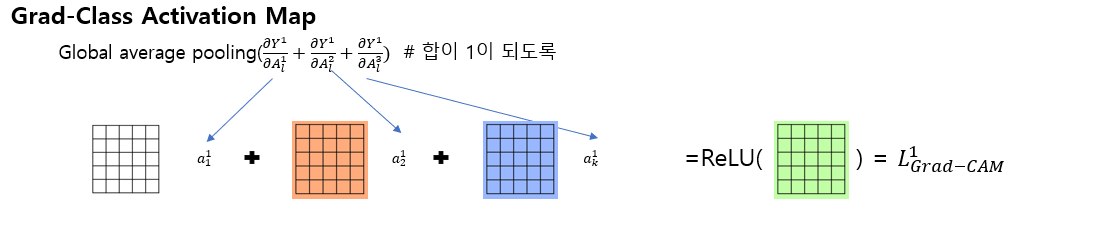
이후, 위의 문제를 개선한 Grad-CAM(2017)이 연구되었습니다. Grad-CAM가중치($a_{k}^{c}$)을 얻기위해서, gradient을 이용하여 아래와 같이 계산합니다. 차이점은 Activation map이($A^{k}_{l-1}$)에서 Activation map($A^{k}_{l-1}$)로 변경되었다는 것과 가중치($a_{k}^{c}$)의 정의가 아래와 같이 변경되었다는 것 입니다. 이 때문에 1) 네트워크의 global average pooling이 꼭 포함될 필요가 없으며, 2) fulley connected layer가 여럿이 포함되어도 됩니다.
$L^{c}_{Grad-CAM}=ReLU(\sum_{k} a_{k}^{c}A^{k}_{l} )$
where $a_{k}^{c}=GP(\frac{\partial Y^{c}}{\partial A_{l}^{k}})$ (GP은 global pooling operation)

Grad-CAM이나 Grad-CAM++이나 가중치($a_{k}^{c}$)을 gradient을 이용해서 정의하여 구합니다. Y(confidence)에 대한 예측을 gradient로 각 채널로 구하는 것이니 fully connected가 몇개여도 가능합니다. 각 채널별로의 중요도를 미분을 이용한 가중치($a_{k}^{c}$)로 구하는 것이죠. 하지만, 이 Grad-CAM도 "채널별 중요도"에 문제가 있습니다.
Gradient을 이용하는 경우의 문제점은 중요도를 정확히 계산할 수 없다는 것입니다. 이 이유를 2가지로 삼습니다: Saturation문제와 False confidence문제
1) Saturation문제는 gradient가 시각적으로 확인할 때, 중요점이 깔끔하게 떨어지지 앟는다는 문제입니다. 딥러닝 네트워크의 gradient가 꽤 노이즈(0이 아닌 소수점이 꽤 많은...)가 있기에, sigmoid function등을 쓰더라도 잔류하는 gradient가 많습니다. 그렇기에 Gradient based 방법론을 쓰면 지저분히 heatmap이 남습니다. sigmoid function 의 입력이 -2라고 하더라도 남고, -5라도 하더라도 뭔가 남고 -10이라고 하더라도 뭔가 소수점이 계속 남습니다.


2) False confidence 문제는 Grad-CAM 자체가 각채널별 Activation map($A^{k}_{l}$)과 가중치($a_{k}^{c}$)의 선형결합이기에, 생기는 문제입니다. Grad-CAM에서는 activaton map의 가중치인 각 i번쨰, j번째 채널에 대해서, 두 가중치$a_{i}^{c}$ > $a_{j}^{c}$가 있는 상황이면 i번째 activation map ($A^{i}_{l}$) 이 더 중요하고, 더 예측에 많이 기여했을거라고 생각합니다. 하지만, 반례가 많이 보인것이 grad-cam의 모습이었습니다. 아래의 그림에서, (2)번의 그림은 가중치($a_{k}^{c}$)가 제일 컷음에도 실제 confidence값 기여에는 0.003으로 낮게 기여한 경우였습니다. 아마도 이 이유를 GP와 gradient vanishing문제떄문이라고 생각합니다. 이 때문에, gradient을 이용하지 않는 해석방법론을 연구한 듯 합니다.

Score-CAM: 모델 컨피던스를 증가시키는 것이 중요도 (Channel-wise increase of confidence, CIC)
모델 컨피던스는 인공지능모델이 예측에 어느정도 강한 예측을 보이는 정도이며 통상 [0, 1]로 정규화해서 얻어지는 값입니다(흔히, 확률이라고 부르기도 하는데 정확히는 확률은 아닙니다). 아무튼 Score-CAM은 이 모델의 반환값(model confidence)가 얼마만큼 증가하는지를 확인하고자하는 것 입니다. Score-CAM은 Increase of confidence의 정의부터 출발합니다.
Increase of confidence의 계산은 베이스라인 이미지에 대비해서 Activation이 활성화된 영역만을 남기고, 나머지부분을 마스킹 했을 때, 예측력이 얼마만큼 confidence을 올리는지 계산하는 방식입니다. 일반적인 CNN이 아니라, 벡터를 넣어 스칼라값을 뱉는 인공지능이라고 생각해서 일반화된 Increase of confidence은 아래와 같이 계산합니다.
$c_{i}=f(X_{b} \circ H_{i}) - f(X_{b}) $
- $ H_{i} $: 이미지랑 같은 크기의 벡터이고, unmasking 용으로 사용됩니다.
*Hadamard Product: 요소별
위의 개념을 CNN에 도입해서 Channel-wise Increase of Confidence (CIC)을 계산합니다.
$C(A_{l}^{k})=f(X \circ H_{l}^{k}) - f(X_{b})$
- $A_{l}^{k}$:l번째 convolution의 k채널의 Activation map을 의미합니다.
- $X_{b}$: 베이스라인 이미지 입니다.
- Up(): CNN이 통과되면서 작아진 사이즈를 다시 원래이미지에 맞춰 업샘플링하는 연산입니다.
- s(): 매트릭스의 원소 값을 [0, 1]로 정규화하는 함수입니다. min-max scaler로 사용합니다. 실제로 activation을 넣어 $A_{l}^{k})=\frac{A_{l}^{k}-minA_{l}^{k}}{maxA_{l}^{k}-minA_{l}^{k}}$로 사용됩니다.
Activation이 얼마만큼 기여하는지 정했다면 이제 Score-CAM을 정리할 차례입니다. Score-CAM이라고 (9)번식이 Grad-CAM과 다르지않습니다. 다만 10번의 가중치($a_{k}^{c}$)가 달라진 것이 큽니다.
$L^{c}_{Score-CAM}=ReLU(\sum_{k} a_{k}^{c}A^{k}_{l} )$ (9)
$a_{k}^{c}=C(A_{l}^{k})$ where C() denotes teh CIC score for activation map $ A_{l}^{k} $

위의 내용을 모두 정리하여, 아래의 알고리즘과 같이 정리할 수 있습니다.
- Activation을 구하기 위해서 X이미지를 딥러닝의 CNN에 forwarding하서 $A_{l}$을 구합니다.
- $A_{l}$개수 만큼 C(채널)을 정의합니다.
- 각 C(채널)만큼 Activation map($A_{l}^{k}$)을 업샘플링하여 원본사이즈에 맞춘 M을 구합니다.
- activation map을 정규화합니다. # $M_{l}^{k}=s(M_{l}^{k})$
- 정규화한 이미지랑 원본이미지랑 요소별 곱하여 리스트 M에 저장해둡니다. // Figure 3의 Phase 1의 완료
- 원본이미지에 Activation을 곱한 것을 딥러닝에 다시 태워서 logit 값의 차이를 구합니다. $S^{c}$
- 채널별로 얻어진 $S^{c}$ 을 softmax하여 합이 1이 되도록 맞춘 가중치 $a_{k}^{c}$을 구합니다.
- Acitvationmap과 선형결합하여 Score-CAM을 구합니다.

결과:
첫 번째 결과로, 정성적(Qualitative)로 사례기반으로 ScoreCAM이 다른 gradient방법론보다 노이즈가 적음을 보여줍니다. 아무래도 gradient 방법론들이 saturation problem이 있기 때문이라고 생각합니다.

두 번째 결과로, 하나의 타깃이 아니라 여러 타깃에도 더 객체를 또렷하게 구분하여 히트맵을 보여주었습니다.

그외에도 Deletetion, Insertion을 픽셀값을 중요도순으로 열거하고, Deletion curve에서는 얼마만큼 성능이 빨리 저하되는지, Insertion curve에서는 중요순으로 추가될수록 얼마만큼 빨리 오르는지를 정량적으로 보여주었습니다. X축 비율, Y축은 AUC입니다.

응용 사례
의학의 적용분야중, 자폐진단에 안저검사이미지가 얼마만큼 예측할 수 있는지 가능성(Feasbility)을 보여준 논문에서도, 이 연구가 정말 가능하다라는 결과를 보여주기위해 Score-CAM을 보여주었습니다. (A)은 이미지를 지워가면서 AUROC을 보여주었고, B은 Score-CAM결과에서 Score-CAM결과를 삭제해가면서 biomedical domain에 의미가 있는 영역이 분류에 중요한지를 보여주는 이미지입니다(링크).

'Data science > Computer Vision' 카테고리의 다른 글
| 색상공간: Color space (RGB, CIEXYZ, CIELAB) (2) | 2024.01.24 |
|---|---|
| [5분 컷 리뷰] CLIP: Learning Transferable Visual Models From Natural Language Supervision (2) | 2024.01.14 |
| [5분 컷 리뷰] SimCLR (A Simple Framework for Contrastive Learning of Visual Representations) 리뷰 (1) | 2023.12.17 |
| [5분 컷 이해] edge detection(에지검출)과 영교차 이론 (0) | 2023.08.22 |
| [이미지 분할] Grabcut 사용법 (0) | 2023.04.26 |



