[5분 컷 이해] edge detection(에지검출)과 영교차 이론

 

 

에지(edge)

---

에지(엣지, edge)은 서로 다른 물체의 경계면에 나타내는 경계선을 의미합니다. 이 경계 주변이 픽셀들의 분포를 생각해보면, 명암의 급격한 변화가 있게 됩니다. 아래의 강아지 사진을 보면, 강아지의 눈을 주변으로 경계는 명암차이가 극명합니다(Figure 1). 이러한 명암차이로, 흰색강아지털과 검은색 눈동자의 경계면을 사람도 인식할 수 있습니다. 에지 검출알고리즘은 이렇듯 명암차이가 극명하게 나는 지점을 추출하기 위한, 여러 연산자(+알고리즘)을 사용하는 것이 공통적입니다.

Figure 1. 포메라니안 강아지

 

 

미분을 이용한 에지의 검출

---

에지의 검출은 명암변화가 급격히 일어나는 지점을 찾는 것이라고 했습니다. 수학적으로는 변화가 급격하게 일어나는 지점을 찾는 것은 미분을 이용합니다. 하지만, 디지털영상에서는 변화가 급격하게 일어나는 지점을 찾으려면 어떻게 해야할까요? 미분을 이용하고 싶지만, 아래와 같이 미분연산에서 극한을 취급할 수 없습니다. 왜냐하면, 디지털영상은 이산형이이기 때문에(=연속이 아님), 미분을 취급하기 어렵습니다. 따라서, 아래와 같이 옆 픽셀과의 차이로 계산합니다.

$f'(x)=\frac{df}{dx}=\frac{f(x+1)-f(x)}{\Delta x}=f(x+1)-f(x)$ (픽셀위치차이를 1로 고려하여)

함수 식은 위와 같고, 이를 영상에 적용려면, 필터(연산자, 커널)를 하나 정할 수 있습니다. 바로 [-1, 1]커널 입니다. 아래와 같이 f(x+1), f(x)인 박스(픽셀)에 [-1, 1] 어레이를 곱하면, 미분값을 구할 수 있습니다. 

하지만, 현실세계에서는 이와 같이 경계면이 확확 바뀌지않습니다. 위의 식으로 아래의 그림(figure 3)의 좌측을 계산한다면, 엣지가 f(x+1), f(x)의 차이가 커서 구분이 잘되겠지만, 우측의 램프엣지(ramp edge)의 형태인 경우는 램프엣지 구간의 명암차이가 일정하게 나타날 것입니다. 그래서, 이 방법론으로는 한계가 있습니다.

Figure 3. 이상적인 엣지(계단형 엣지)와 램프엣지의 형태 (10.14445/22312803/IJCTT-V23P110)

 

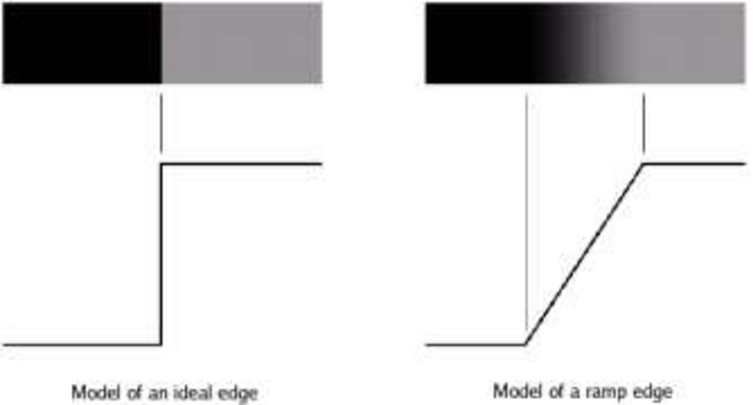
하지만, 1차미분이아닌 2차미분을 이용하면 램프엣지(ramp edge)에서도 경계면을 찾을 수 있습니다. 아래의 그림의 좌측(Figure 4), 램프엣지가 있다고할 때, 이 명암의 크기는 우측상단의 그림처럼 보여질 것 입니다. 그리고 이를 1차미분하면 위의 블록이 하나 있는 것처럼 보이는 봉우리가 나타날 것입니다. 그리고, 여기서 한번 더 미분한 (2차미분) 값을 구하면, 1차미분에서 봉우리의 시작점, 출발점 사이의 가상의 선이 무조건 0을 지나게됩니다. 즉, 2차 도함수를 이용하여, 영교차(zero-crossing)하는 지점을 찾으면, 램프엣지에서도 경계선을 찾을 수 있습니다.

Figure 4. 램프엣지에서의 경계구하기 https://www.52coding.com.cn/2018/12/04/RS%20-%20Recognizing%20Image%20Features%20and%20Patterns/

위의 영상은 1차원의 공간에서 명암을 기준으로 했기에, 이제 2차원으로 확장해봅니다. 단순히 1차원을 2차원으로 확장하면, x, y축에서의 미분값을 구하면됩니다. 그 식은 아래와 같습니다. 1차도함수 먼저 정의하고, 1차도함수를 2번사용하면 2차도함수를 구할 수 있습니다.

$\nabla f(y,x)=f'(y, x)=(f(y+1, x)-f(y,x), f(y, x+1)-f(y,x))= (d_{y},d_{x})$

하지만, 실제로는 잡음이 있어서 위와 같이 픽셀 하나차이의로만은 노이즈가 있어, 두 픽셀 사이로 영교차 이론을 적용합니다. 그렇기에 실무적으로 쓰이는 공식은 아래와 같습니다.  이렇게 되면 실제 마스크(kernel)은 [-1, 0, 1]와 같은 커널을 적용할 수 있습니다.

$\nabla f(y,x)=f'(y, x)=(f(y+1, x)-f(y-1,x), f(y, x+1)-f(y,x+1))= (d_{y},d_{x})$

위와 같이 엣지를 구할 수 있으면, 추가적으로 다음의 두 개념(엣지강도, 그레디언트 방향)을 구할 수 있습니다.

• manitude($\nabla f(y,x)$) = $\sqrt{d_{y}^{2}+d_{x}^{2}}$
• Gradient orientation: $ \theta = tan^{-1}(\frac{d_{y}}{d_{x}}) $

 

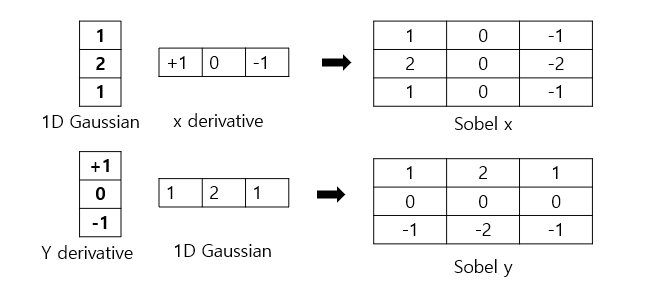
Sobel filter: 1차원 가우시안 필터(Smoothing)을 이용한 필터  + 미분

---

현실세계에서는 필터를 적용할 때, 이미지의 픽셀이 노이즈가 많기 때문에 이를 리덕션해줄 필요가 있습니다. 가우시안 필터는 이러한 경우 흐릿하게하는 블러(blurring)에 사용되는데요. 소벨필터는 이 가우시안 필터와 x,y 축별로의 그레디언트를 혼합하여 사용하는 필터입니다. 그렇기에 상대적으로 노이즈에 덜 민감한 편입니다.

Sobel filter 및 분해

 

 

Prewitt operation: 평균필터 + x,y 미분

---

프레윗 연산은 소벨과 다르게, 평균으로만 스무딩필터를 적용합니다. 그 결과 아래와 같은 커널을 얻을 수 있습니다.

Prewitt filter 및 분해

[1] https://theailearner.com/tag/cv2-sobel/