[5분 컷 이해] Multiple Instance learning 이란?

 

요약

---

요약: Supervised learning의 일반적인 개념으로, Supervsed learning에서는 분류하고자할 instance가 정확히 True/False 등의 라벨이 필요한데,Multiple instance learning에서는 Instance까지는 True/False 까지는 안되어있어도, Instance의 묶음(Bag) 내에 True가 있을까? False일까를 맞추는문제. 주로 탐색해야할 영역들이 넓은 Pathological image, Document classification에 사용된다. 

 

Fig 1. MIL과 Single instance learning 과의 차이(이미지: Multiple instance learning for histopathological breast cancer image classification)

 

 

 

 

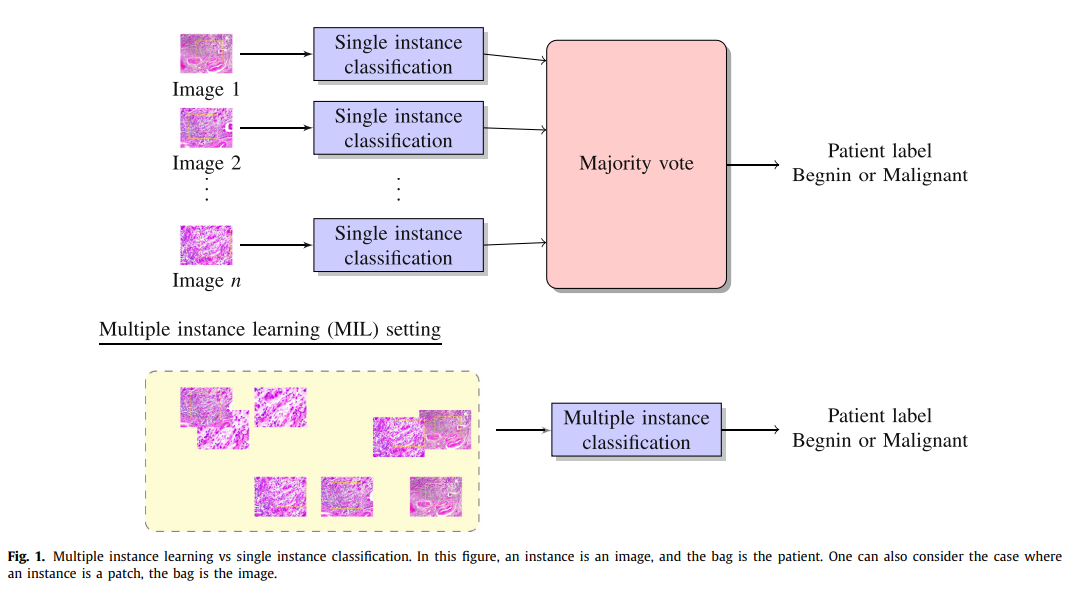
입/출력에 대한 상세: 입력값의 형태, 출력값의 형태, 문제는 어떤형식인가?

---

구체적으로는 각각의 instance까지의 라벨은 안되어도, instance을 포함하는 bag들의 라벨만 있으면 되는 형식이다 [1]. 보통 이걸 Weakly labling되었다고 한다

수식으로 보면 아래와 같다 [2].

• $B_{n}$: Whole Slide Image(WSI)을 하나의 Bag이라고 가정한다 
• $B_{n} = (x_{1}, x_{2}, x_{3}, x_{4},...,x_{n_{i}}), \omega_{n}$ : n번째 WSI을 하나의 Bag이라고 생각하면, 이 WSI내에는 각각의 패치를 $x_{n}$이라고 할 수 있다. 이 패치는 WSI이미지 마다 개수가 다를 수 있으므로 $x_{n_{i}}$ 라고 서브스크립트를 달아 놓았다.
• $\omega_{n}$: 이러한 n번째 WSI는 각각의 라벨이 존재한다. 예) 악성종양/양성종양 
• $p(\omega|B_{n})$: 전체 WSI내에 여러 이미지를 하나의 bag으로 주었을 때, 라벨을 맞추는 문제.
• $p(\omega|B_{n})= E[p(\omega|x_{i})] \forall x_{i} \in B_{n}$: 어떤 인스턴스(x)가 들어와도 라벨의 잘 맞출 확률
• $\omega = max_{k}\left \{ y_{n_{i}} \right \}$: bag내에 $n_{i}$개 중, 모든라벨이 0이어야 bag의 라벨이 0, 하나라도 1일경우에는 1을 의미한다.

VGG을 이용한 MIL모델의 예시. 이미지 소스: MULTIPLE INSTANCE LEARNING OF DEEP CONVOLUTIONAL NEURAL NETWORKS FOR BREAST HISTOPATHOLOGY WHOLE SLIDE CLASSIFICATION

 

실제 구현 예시

---

tensorflow로 구현

 

 

 

언제쓰면 적절한가?

---

1. 각 인스턴스의 라벨을 직접 다는 것이 너무 어렵지만, bag의 라벨은 달 수 있을 때(Weakly labled)
2. 큰 이미지를 다룰 때,
3. 다운샘플링(Donwsampling)이 불가능할 때

 

 

MIL 사례 연구들 

---

- 사례 1: Document에서의 사례 [1]

- 문제: 문서가 이미지로 들어올 때, 관련 문서인지 파악하는 문제
- Supervised로 한다면?: 문서에는 로고, 시그니처, 그림, 테이블 등이 포함되어서 global descriptor로 풀기가어려움.
따라서, 이미지를 각각의 여러 zone으로나눈후, 각각의 zone에 대한 분류로 나누고자함. 분류기가 Document = [zone1, zone,2 zone3, ... zone N]라고 생각해서 각각의 zone 중에 한 영역만 True여도 관련분야다라고
학습시키려고 한다는 것이다. 그럴려면 사실 각 zone에 대해서 많은 label이 필요한데 비용이 많이든다.

 

 

- 사례 2: Histopahtological Image (조직병리학적 이미지) 슬라이드에서의 암예측

Camelyon7 Challenge (breast ca): 병리이미지를보고 환자가 전이성암이 될 것인가 말것인가를 푸는문제, PANDA challenge (prostate ca): prostate ca의 점수를 계량할 수 있는 점수(Gleason score)을 예측하는 것

 

 

 

- 사례3: Classifying and segmenting microscopy images with deep multiple-instance learning [3, 4]

instance-based MIL형태에 속하는 연구이다. 각 instance에 대해서 분류기를 통과시키고, 이를 다시 aggregation하는 형태로 동작함. aggregation하는 함수를 global pooling layer라고하는데, 이 연구에서는 Noisy-and pooling function이라는 것을 만들었다. 가정은 Bag이 Positive이면, Bag내의 인스턴스가 Positive인 것들이 일정 threshold을 넘길것이라는 가정을 둔다. 

1. $p(t_{i}=1 | x_{j})$: Bag내에 인스턴스 $x_{j}$을 인자로 받았을 때, $t_{i}$클레스일 확률을 구하는 분류기
2. $g(\cdot)$ (global pooling function): noisty-OR 이라고 함. 집계한 확률을 내어주는 함수. $p(t_{i}=1 | x_{1},...x_{N})$. 좀 다르게 표현하면, 각 인스턴스의 확률을 집계하여, Bag이 i라벨에 속할 확률을 구해주는것. $P_{i} = g(p_{i1}, p_{i2}, ...P_{iN}):
3. Noisy-AND: $P_{i}=g_{i}(p_{ij}) = \frac{\sigma(a_{p_{ij}-b_{i}}) - \sigma(-ab_{i})}{\sigma(a(1-b_{i})) - \sigma(-ab_{i})}$. 이 식의 $a$은 sigmoid function전에 입력값을 multiple할 때 쓰고, $b_{i}$은 적어도 몇개가 있어야하는지에 대한 threshold로 역할을 한다.

 

$g(\cdot)$(global pooling function)을 어떻게 하냐에 따라 종류가 많은데, 대체적으로 아래와 같이 알려져있음.

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4908336/pdf/btw252.pdf

 

실험에서는 MNIST dataset은 concat시켜서 만들어, MIL의 분류기를 만드는 시험을 했다. 라벨이 2라면 2가 적어도 b개만큼 있어야한다는 Noisy-AND을 이용하여 학습한다.

 

 

 

Reference

---

[1] : https://www.academia.edu/download/78345586/Kumar_ICDAR_2011.pdf

[2]: MULTIPLE INSTANCE LEARNING OF DEEP CONVOLUTIONAL NEURAL NETWORKS FOR BREAST HISTOPATHOLOGY WHOLE SLIDE CLASSIFICATION

[3] https://github.com/dancsalo/TensorFlow-MIL

[4] https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4908336/pdf/btw252.pdf