연금술사

Doc2vec, Word2vec처럼 각각의 단어를 벡터로 표현하고자하는 시도가 꽤 있어왔다. 이런 벡터표현은 단순히 bag-of-words으로 표현하거나, one-of-k (흔히 one-hot vector)라고 부르는 방법으로 표현할 수 있다. 그러나 이러한 시도들은 여러 문제가 있었고, word2vec으로 더 밀도있는 표현방식(denser representation)을 사용했다. 한 단어를 doc2vec으로 임베딩하여 표현할 수 있었듯이, document 또는 paragraph을 벡터로 표현할 수 있는데 왜 supervised paragraph2vec가 필요한건가? 이에 대한 장점은 있는건가? 이에 대한 대답을 Supervised Paragraph Vector: Distributed representations of words, documents, and class에서 찾을 수 있다.

Supervised paragraph vector가 필요한 이유?

범용적인 임베딩모델(예, doc2vec, paragraph2vec 이하 PV)은 정말 단순한 알고리즘으로 hidden layer가 하나만 존재하여 매우 학습이 편하고, 쓰기도 편하지만, 임베딩에 다음과 같은 문제가 있다. word2vec의 CBOW(continous bag of words)을 생각하면, 단어벡터(word vector, 단어를 임베딩한 벡터)를 구문론적(syntactical)으로 학습하기도하고, 의미론적(semantic)적으로 학습하기도 한다. 예를 들어, "the cat sat on the mat"이라면, cat을 예측할땐, 주변단어인 the와 sat을 이용해서 예측한다. 따라서 유사한 단어가 동시에 많이 출현될수록, 같은 벡터로 표현될 확률이 높고, 주변단어의 쓰임이 비슷하게 나왔을 때도, 유사한 벡터로 임베되는 경향이 있다 (Figure 1. A). 하지만, 해결해야하는 문제가 감정분석(sentimental analysis)로, wonderful과 amazing이 같은 그룹으로, terrible, awful이 부정그룹으로 분리되서 해야한다면 어떨까? 동시출현 또는 유사한 단어가 많이 출현하는 것을 학습하여 임베딩하는 word2vec의 이런 학습방식은 특정테스크에 모두 걸맞게 쓰기가 쉽지가 않다. 이런 일반화된 분석방법으로는 이런 임베딩의 표현의 의사결정바운더리(decision boundary)을 긋기가 쉽지않다. 본 논문은 word2vec, paragraph2vec, doc2vec의 제한점을 해결하고자 시도했던 논문이다. 

word2vec의 출력에이어의 

SPV의 핵심 아키텍처

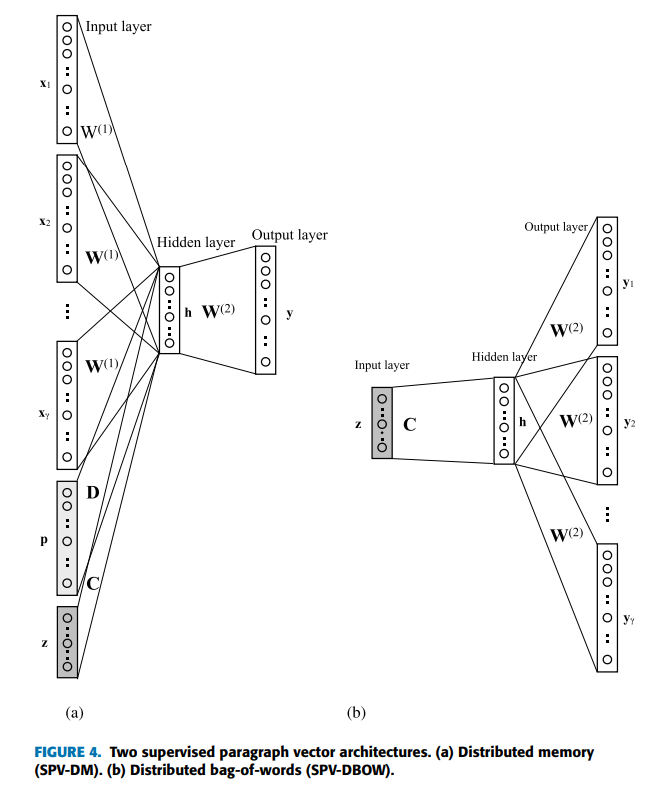
해결방법은 다음과 같다. word2vec의 아키텍처와 같이 하나의 입력레이어, 하나의 히든레이어, 하나의 출력레이어로 구성한다(Figure 4-A). 좌측에 아키텍처의 구성을보면, $x1,..., x_{\gamma}$까지는 한 문단에 들어가있는 단어가 one hot vector로 변환된 벡터를 의미한다. 각각 one-hot vector로 표시할 때, 총 단어의 개수가 V라면, V개 원소의 개수를 가지고, 원소중 하나만 1인 벡터가 된다. 차이점이라면, 다음과 같은 벡터들도 입력값에 전달된다. 바로 도큐먼트의 one-hot vector인 $p$와 클레스의 라벨인 $z$가 추가로 전달된다는 것이다. 아래의 그림에서는 $p$은 전체 문서(documents)의 수를 의미한다. $z$은 클레스라벨을 의미해서, $M$개의 클레스가 존재한다고 했을 때, 각각 하나하나를 one-of-K(one-hot)벡터로 인디케이팅한 것을 의미한다. 그리고 h에 해당하는 히든레이어의 출력을 $\delta$개의 원소를 가진 벡터라고하자.

위와 같이 셋팅한 경우, $W^{(1)}$은 임베딩을 위한 dense layer의 가중치 메트릭스로 $\mathbb{R}^{V\times\delta}$가 된다(V개의 one-hot vector을 $\delta$개로 압축하는 fully connected layer 이기 때문). $W^{(2)}$은 출력레이어의 가중치로 W1의 전치행렬과 크기가 같다(왜냐하면, 출력해야하는 단어도 V개의 벡터여야 하기 때문이다). 

위의 아키텍처에서 목적함수를 클레스라벨이랑 도큐먼트의 인덱스 단어에 최대한 학습할 수 있게 다음과 같이 정의하였다. 

1. SPV-DM(여러 단어가 주어진 경우, 한단어를 예측하는문제):  아래의 우변의 시그마 내 첫 항은 "CBOW와 같이 주변단어가 주어졌을 때, 예측하고자하는 단어를 예측하기위한 손실함수", 두 번째 항은 "문서내에 해당 예측하고자 하는 단어가 있을 확률", 세 번째 항은 "문서의 라벨이 주어졌을 때, 해당 단어가 있을 확률"을 모두 더한 값이다.

$L_{SPV-DM} = \frac{1}{T}\sum_{t=1}^{T}\sum_{j=1}^{\gamma}log(p(w_{t}|w_{t+j})+log(p(w_{t}|d))+log(p(w_{t}|c)))$

2. SPV-DBOW(한 단어가 주어진 경우, 여러단어를 예측하는 문제)

$L_{SPV-DBOW} = \frac{1}{T}\sum_{t=1}^{T}\sum_{j=1}^{\gamma}log(p(w_{t+j}|c))$

논문에는 등장하지 않는 limitations

1. 본 모델은 word2vec에 사용되는 모델과 구조가 유사해서, OOV(out of vocabulary)의 문제를 그대로 갖고있다. 따라서 unseen data에 대해서는 모델이 강건하지 않을 수 있다.

Summary: BERT(Bidirecitonal Encoder Representations from Transformer)

사전학습이 된 양방향 표현법으로 각 모든레이어에서 우측과 좌측의 문맥정보(context)을 결합하는 것을 사용하는 언어모델이다. BERT는 Transformer의 목적함수가 변형된 형태이다. 이전 개발된 Transformer에서는 이전단어들을보고 다음단어를 예측하는 Uni-directional(일방향)의 언어모델이었다면, BERT은 다음의 차이가 있다.

• 사전학습을 양방향으로 해서, 문맥정보를 더 파워풀하게 학습 (=Deeply bidirectional. 예, 나는 밥을 ???.    ???->밥을->나는) (Transformer와 유사한 언어를 인코딩해서 압축하는 형식이나, Transfoermed은 한번에 모든 단어들은 한거번에 보지만, BERT은 left-to-right, right-to-left순차적으로 본다)
• 사전학습시에 Pre-traniing 과 fine tuning을 두 단계를 모두 활용하는 형식(BERT은 2가지의 손실함수를 가지고있고, 이 두 가지의 손실함수의 합을 손실함수로하여 동작한다)

Introduction

Pre-training: 대용량 데이터를 일단 학습시켜놓고, 이후에 재학습하는 것을 의미한다. 이러한 사전학습으로 튜닝하는 방식은 크게 두가지로 나뉜다.

1. Feature-based (Parameters are fixed): 파라미터를 고정시켜놓고(e.g. tensorflow에서는 freezing). e.g) ELMO
2. Fine-tuning (Parameters are not fixed): 특정 테스크에는 굉장히 적은 파라미터. GPT 계열이나 Uni-directional 언어모델.

그런데, 여태까지 이런 접근법은 언어를 표현하기위해, 1) 단방향의 언어를 사전학습(예, 좌측에서 우측으로만 단어를 예측), 2) 파라미터를 고정하든 안하든 같은 목적함수를 가지고 사전학습을 한다. 

=> 저자들은 이러한 기술이 사전학습을 더 잘 쓸수 있는것에 오히려 제한을 둔다고 얘기한다. 특히, fine-tuning을 하는 방법에서는 더욱 그렇다고 얘기한다 (아마도, 글자는 좌측에서 우측으로만 예측해야하니까, 반대로 우측에서 좌측으로 이해해서 얻을 수 있는 단어들 ([] 먹었다) 이런 정보들도 활용을 못하지 않나?) 생각이든다. 저자들도 가장큰 단점은 단방향모델이 가장 단점이라고 하고 있다(The major limitation is that standard language models are unidirectiona). GPT2 같은 경우도, sentence level task(문장단위의 예측모델)이나 token level task(예, question anwering)에서는 최적의 성능을 보여주지 못했는데, 양방향의 문맥정보를 활용하지 못했기 때문이라고 한다.

BERT는 Transformer의 목적함수가 변형된 형태이다. 특히, fine-tuning based approaches이다. 그리고, 단방향의 단점을 개선한 MLM(Masked language model)이다. 즉, 이전 개발된 Transformer에서는 이전단어들을보고 다음단어를 예측하는 Uni-directional(일방향)의 언어모델이었다면, BERT은 양방향으로 파악한다는 것이다.

. BERT은 2가지의 손실함수를 가지고있고, 이 두 가지의 손실함수의 합을 손실함수로하여 동작한다.

손실함수의 종류는 다음과 같다.

1. Loss function 1: BERT은 문장에 15%정도를 Masking을 해놓고, 처리한후에 masking된 단어를 에측하는 방법에 관한 손실함수를 가지고 있다. (일종의 CBOW다). 다만, CBOW와의 차이점은 양방향으로 단어를 예측한다. 
2. Loss function 2: 문장들 사이에 관계를 학습하여, 주어진 문장과 다음문장이 연속된 문장인지 문맥을 학습(contextual)할 수 있게끔 손실함수를 설계했다. 예를 들어, 문장A가 문장B와 연속된 문장인지? 아닌지를 학습하기위한 장치를 마련했다. 다음 문장이라는 라벨링을 추가했다. 

Pre-requisite

Pretraning language model은 어떤것들이 있어왔고, 어떤 제한점이 있었는가?

1. Unsupervised feature-based approaches: 주로 좌측에서, 단어들을 임베딩하기위해사용되었고, 우측으로 언어모델링을 하는 방법들이 많이 사용되었거나(Mnih and Hinton, 2009), 좌측의 잘못 입력된 단어들과 우측의 문맥으로 단어들이 적절하게 쓰였는지 판단하는 목적으로 주로 쓰였었다. 이 접근법들은 일반화되면서, 문장을 임베딩하는 방법이나(Kiros et al., 2015; Logeswaran and Lee, 2018), 문단을 임베딩 하는 방법들로도 사용되었다s (Le and Mikolov, 2014). 예를들어, 문장(senstence)을 표현하기위해서는 다음 문장들 어떤게 적절한지 적절한 문단을 훈련하는 목적함수를 갖게 사용했거나, 좌측의 단어들이 있을떄, 다음문장을 생성(generation)하는 방법, 또는 오토인코더에 사용되는 목적함수들이 사용되었다. ELMo와 이전세대들이 에애 해당한다. 2017년~2018년에 개발된 ELMo은 전통적인 단어임베딩을 위해 쓰였고, 좌측->우측과 우측->좌측의 다른 언어모델로부터 문맥정보를 담은 feature들을 추출해냈다. 그 다음에 left-to-right, right-to-left표현을 단순히 concatenatation시켜서 이 특징값을 사용했다. ELMo와 유사하게, 다른모델들도 있었는데 단순히 feature based으로 사전학습했지만, deeply bidrectional을 사용하진 않았다. 
2. Unsupervised Fine-tuning approaches: 유사하게, 사전에 학습된 가중치에 목적에 맞게 모델의 가중치 전체를 다시 학습하는 방법으로는 단어를 표현한는 방법으로는 2008년에  연구(Collobert and Weston, 2008)가 시작되었다. 이후에는 일단 인코더에서 문장이나 문서를 임베딩한 후에, 목적에 맞게 재학습하는 연구들이 2015~2018년에 주로 있었다. 이러한 접근법의 가장 큰 장점은 스크레치(scratch) 모델의 적은수의 파라미터만 다시 재학습된다는 것이다. 이에 해당하는 것이 OpenAI GPT, GLUE에 해당한다.
3. Transfer learning from supervised data: 자연어, 기계번역등에서의 많은 연구들이 이에 해당한다. 

본문

BERT은 크게 2단계의 프레임워크의 순서를 따른다. 첫 번째는 pre-tranining, 둘 째로는 fine-tuning이 이에 해당한다. 사전 학습때는 모델은 여러 테스크에 적용하기위해서, 라벨이 없는 데이터셋(비지도학습)을 학습한다. 그 후, fine-tuning단계에서는 BERT model을 초기파라미터가 세팅된후에, 모든 파라미터를 다시 목적에 맞는 테스크(down stream task)를 위해 재학습한다.

아래의 그림처럼, 출력부문을 제외하고는 같은 모델을 쓴다. 그러나, 출력부도 초기에는 BERT가 사전학습된 파라미터로 초기세팅이 이뤄진다. 가장 두드러진 특징은 BERT은 어떤 목적의 테스크든, 동일한 아키텍처라는 것이다. 즉, pre-tranied model의 아키텍처와 final downstream model가 거의 차이가 없다는 것이다.

• 모델: 모델은 multi-layer bidirecitonal transformer encoder이다. Transformer은 2017년에 개발된 transformer을 이용했다. Transformer의 적용은 거의 동일하고, 파라미터 사이즈들만 좀 다르다. BERT base은 GPT등 성능비교를위해 만들어낸것들이고 BERT Larget은 꽤 큰 사이즈의 파라미터를 가진 모델이다.
• 입출력의 표현: 이 모델은 다양한 downstream task을 쓰기위해서, 명확한 표현이 필요하다고 한다. 입력은 1개의 문장 또는 2개의 문장인데, 따로 묶인 형태로 입력값이 전달된다. 모든 문장에서의 첫토큰은 문장의 시작임을 알려줄수 있는 CLS라는 스페셜한 토큰을 전달해준다. 만일 두개의 문장이라면 두 문장을 이어붙인 후에 하나의 CLS 토큰을 부여한다. 이 문장이 그럼에도 다른문장임을 나타내기 위해서는 스페셜 토큰을 하나 붙여주는데 [SEP] 토큰이다.
•  

Pre-tranining BERT

손실함수의 종류는 다음과 같다.

1. Loss function 1: BERT은 문장에 15%정도를 Masking을 해놓고, 처리한후에 masking된 단어를 에측하는 방법에 관한 손실함수를 가지고 있다. (일종의 CBOW다). 다만, CBOW와의 차이점은 양방향으로 단어를 예측한다. 
2. Loss function 2: 문장들 사이에 관계를 학습하여, 주어진 문장과 다음문장이 연속된 문장인지 문맥을 학습(contextual)할 수 있게끔 손실함수를 설계했다. 예를 들어, 문장A가 문장B와 연속된 문장인지? 아닌지를 학습하기위한 장치를 마련했다. 다음 문장이라는 라벨링을 추가했다. 

예를 들어, 아래와 같다. 연속적인 문장인 경우는 라벨을 True, 아니면 False

RNN계열에서도 Bi-direcitonal RNN(=shallow)도 가능하지 않은가?

정답은 Yes이다. RNN계열에서도 bi-directional RNN으로 예측하고자하는 Y을 양방향으로 예측한다. 아래의 그림과 같이 Bi-directional RNN은 "The results clearly show that"의 첫 번째 토큰인 The을 이용해서 예측값을 만들고자할때, reverse된 문장의 가장 첫 번째 단어인 "that"의 결과값과 concat시킨 후에 softmax을 적용해서 예측한다. 즉 LSTM의 unit이 d이면, 반환되는 hidden state의 vector size가 2d가 된다.

Key contribution

• We cast few-shot learning as a supervised message passing task which is trained end-to-end using graph neural networks.

• We match state-of-the-art performance on Omniglot and Mini-Imagenet tasks with fewer parameters.

• We extend the model in the semi-supervised and active learning regimes

=> 그레프에서 노드분류에 많이 사용되는 메시지 패싱(A노드를 분류하고자할 때, A와 인접한 노드의 라벨을 참조하여 라벨을 예측하는 방법)을 이용해서 few-shot을 진행함. 위의 전략으로 실제 데이터 Omnigolot(알파벳분류), 이미지분류(Mini-imagenet)에서 우수한 성능을 보임. 이 모델을 준지도학습과 엑티브러닝에 확장함.

Problem setting

아래와 같이 입력값(T)과 출력(Y)가 있다고하자. T을 자세히보면 s까지 x와 l개가 있는데, 이는 라벨이 있는데이터가 s개가 있다는 것이다. 그리고 x_r까지 있는 데이터는 라벨이 없는 입력값이며, x_t은 분류하고자하는 test data이다. l의 라벨은 K개로, 멀티라벨분류문제이다. 또한, 각 입력x끼리는 독립적이며, 같은분포p 에서 나왔다고 가정한다(=train, test split가 랜덤하게 주어진것과 비슷한 상황).

Y는 x_t의 라벨을 의미한다.

이런 데이터셋에서 다음의 3가지의 문제가 등장한다.

1.  Few shot learning: r=0 (라벨이 없는 데이터는 없으며), 라벨이 있는 데이터만 있고, 예측해야할 데이터가 1개일 경우(t=1). 그리고, 훈련데이터 샘플의 개수인 s 가 비교적 넉넉하여 s=qk 인경우. 예를 들어 예측해야할 라벨(K=5) 5개인데, q=10이어서, 데이터가 50개인경우를 의미한다. 이러한 경우는 10-shot, 5 way learning이라고 한다.

2. Semi-supervised learning: r>1 인경우여서, 라벨이 없는 훈련데이터세트가 존재하는 경우를 의미한다. 위의 문제는 같이 훈련데이터 내 라벨이 있든,없든 같은 분포에서 x가 나왔기 때문에, 라벨이없는데이터를 최대한 활용하는 것을 목표로 한다. 주요한 가정은 x와 x'(라벨이없는데이터)는 같은 분포에서 나왔기 때문에, 둘은 같은 라벨일 것이다라는 것이 주요 가정이다.

3. Active learning: 모델이 학습하고자하는 데이터의 라벨을 인간에게 요청하고, 계속학습하는 학습방법. Semi-superivsed의 특별한 경우라고 생각되며, s+r << s0 , S <<S0. 라벨이 없는 학습데이터의 개수보다 라벨이 있는 학습데이터의 개수가 충분히큰 상황. 본 연구에서는 semi-supervised보다 active learning이 얼마나 더효과적인지를 분석하고자한다.

- 몇가지 배경지식이 필요하다. Human In The Loop (HITL)은 컴퓨터는 빠르고, 정확하지만, 문제를 푸는 방법은 멍청하고, 인간은 느리고, 똑똑하지만 문제푸는 방법은 현명하다. 이 둘을 머신러닝 학습에 혼합하는게 HITL이라는 개념이다. 사실 모든 기계학습과정은 HITL의 연속이다. 예를 들어, 사소한 하이퍼파라미터만 해도 사람의 과정이 들어가기 때문이다. Active learning은 이 HITL에서 인간의 개입이 명시적으로 들어간 반복적인 작업이다. 

1. Oracle(인간)이 모델과 라벨이 있는 데이터를 생성함. ground truth을 제공하는 원천. 라벨러+ 모델생성자로 생각할 수 있음.
2. 모델은 오라클이 준 라벨을 학습함. (추가적으로 인간이 준 검증용 데이터 세트에 학습로그를 제공)
3. 모델은 데이터에 라벨을 붙이고자하는 라벨없는 데이터를 인간에게 요청함
4. 이 과정을 반복

모델링

기본적으로 언어는 계층구조를 갖는다. 구(Phrase)와 절(Clause)처럼 단어가 모여서 구(phrase)을 이루고, 구가 모여서 절(clause)을 이룬다. 예를 들어, 형용사절을 들어본적이 있는가? "men in black"과 같이 "in black"이 형용사절을 이루고, 이러한 구가 모여서 명사절 등을 이룬다. 사람은 이와 같이 계층구조를 이루는 것을 이애할 수 있다. 유사하게, "이런 계층구조의 모델링을 명시하진 않았지만 Tree 구조를 이용한다면, 더 좋게 할 수 있지는 않을까"에 대한 질문이 본 페이퍼의 핵심이다.

본 페이퍼를 읽기 위해 다음의 배경지식이 필요함

1. Inductive bias (aka learning bias): 귀납적 편향. 학습편향. 모델이 경험하지 않은 데이터를 입력받았을 때, 출력을 예측하는데 사용하는 가정의 집합임. 정확히 학습되지 않은 것들을에 대해서 귀납적으로 학습한 것들이 있으니, 예측을 할 수 있지 않느냐의 대한 가정임. 

=> 본 연구에서는 이러한 학습편향을 정보의 주기(생성~삭제)를 따로따로 관리하여(differentiation) 증진하겠다는 전략이다. High ranking neuron과 low ranking neuron으로 나눠서, 고순위의 뉴런들에서는 정보를 오래 가지고 있게하고, 저순위 뉴런에서는 정보를 빨리 잊게하는 테크닉을 보임.

Key technique: ON-LSTM

1. Cumax: Cumax은 Cumsum(cummulative summation)과 softmax을 합친것이다(합성함수다). 이를 사용하는 이유는뉴런의 랭킹을 결정할때 지나치게 명확히 high, low랭킹을 구분하는것을 피하기위해 사용되었다고한다. " To avoid a strict division between high-ranking and low-ranking neurons, we propose a new activation function, the cumulative softmax, or cumax(), to actively allocate neurons to store long/short-term information". Cumax에서 반환되는 값은 누적합이기에 연산도중에 1이뜨면, 그 이후의 인덱스의 값들은 모두 1일 것이다. 따라서, 어느 인덱스부터 1인지에 대한 기준이 되는 지를 표기했는데, $d_{t}^{f}$이다.

import tensorflow as tf

# Equation (6)
def cumax(x, axis=-1):
    return tf.math.cumsum(tf.nn.softmax(x, axis), axis)

def split_point(x):
    x = x.numpy()
    return np.where(x == 1)[0].min()

2. LSTM : Ordered neuron LSTM은 기본적인 LSTM연산을 필요로하고, 그 위에다가 master gate을 부착한다. 그렇기에 LSTM연산도 포함된다.

    
class ONLSTM(tf.keras.layers.Layer):
    def __init__(self, input_dim, hidden_unit):
        super(ONLSTM, self).__init__()
        self.input_dim = input_dim
        self.hidden_unit = hidden_unit
    
    def build(self):
        # Equation 1-5: basic LSTM model
        self.w_f = self.add_weight(shape=(self.input_dim, self.hidden_unit), name='standard_lstm_kernel')
        self.w_i = self.add_weight(shape=(self.input_dim, self.hidden_unit), name='lstm_input_kernel')
        self.w_o = self.add_weight(shape=(self.input_dim, self.hidden_unit), name='lstm_output_kernel')
        self.w_c = self.add_weight(shape=(self.input_dim, self.hidden_unit), name='cell_memory_kernel')

        self.u_f = self.add_weight(shape=(self.hidden_unit, self.hidden_unit), name='standard_recurrent_kernewl')  # u_f
        self.u_i = self.add_weight(shape=(self.hidden_unit, self.hidden_unit), name='lstm_input_recurrent_kernel')
        self.u_o = self.add_weight(shape=(self.hidden_unit, self.hidden_unit), name='lstm_input_recurrent_kernel')
        self.u_c = self.add_weight(shape=(self.hidden_unit, self.hidden_unit), name='lstm_input_recurrent_kernel')

        self.b_f = self.add_weight(shape=(1, self.hidden_unit), name='forget_bias')
        self.b_i = self.add_weight(shape=(1, self.hidden_unit), name='input_bias')
        self.b_o = self.add_weight(shape=(1, self.hidden_unit), name='output_bias')
        self.b_c = self.add_weight(shape=(1, self.hidden_unit), name='cell_bias')
        
        
   def _base_lstm_op(self, x, h):
        f_out = tf.nn.sigmoid(tf.tensordot(x, self.w_f) + tf.tensordot(h, self.u_f) + self.b_f)
        i_out = tf.nn.sigmoid(tf.tensordot(x, self.w_i) + tf.tensordot(h, self.u_i) + self.b_i)
        o_out = tf.nn.sigmoid(tf.tensordot(x, self.w_o) + tf.tensordot(h, self.u_o) + self.b_o)
        c_out = tf.nn.tanh(tf.tensordot(x, self.w_c) + tf.tensordot(h, self.u_c) + self.b_c)
        return o_out * tf.nn.tanh(c_out)

3. ON-LSTM: strucure gate mechanism:

    def call(self, x, h):
        h, outputs = self._base_lstm_op(x, h)

        lstm_f = outputs[0]
        lstm_i = outputs[1]
        lstm_c_hat = outputs[2]


        # Equation 9: master forget gate.
        wx = tf.einsum('ij,jk->ik', x, self.w_f)  # (1xhidden)
        uh = tf.einsum('ij,jk->ik', h, self.u_f)  # (1xhidden)
        f_t = cumax(wx + uh + self.b_f)  # (1 x hidden)

        # Equation 10: master input gate.
        i_t = 1 - cumax(wx + uh + self.b_i)  # (1 x hidden)

        # Equation 11:
        w_t = f_t * i_t #  (1 x hidden)

        # Equation 12:
        f_t_hat = f_t * (lstm_f * i_t + 1 - i_t)

        # Equation 13:
        i_t_hat = i_t * (lstm_i * f_t + 1 - f_t)

        # Equation 14: first d_t neuron of the previous cell state will be complete erased.
        c_t = f_t_hat * self.c_t + i_t_hat + lstm_c_hat
        self.c_t = c_t

        return h

Reference: https://openreview.net/forum?id=B1l6qiR5F7

GAT(Graph attention network)은 생각보다 오래전에 나왔다. 2018 ICLR(International Conference Learning Representation)에 발표되어, 현재 인용수만해도 3,000이 넘는다.

Key technical contribution

이전 그레프의 상태를 다음 그레프 상태에 Self-attention을 적용하여, 이전 그레프의 노드에 대한 다음 그레프의 노드의 중요도를 파악하는 것. 이를 attention coefficient 이라고함.

Attention coefficient: 아래와 같이 $h_{i}$(i번재 상태에서의 특징값)을 $h_{j}$번째의 상태에서의 특징값에 대해서 self-attention함. 결국 다음의 식에 따라, self-attention을 돌리고, 마지막에 attention weight을 곱하여, i번째의 상태의 그레프의 특징값을 반환

Multihead-attention coefficient: 저자들은 위의 attention coefficient을 k개를 만들어서 concat하는 방법으로 Multi-head attention을 계산도 해봄.

Single attention만 코드로 간략히 핵심만 구현하면 다음과 같다.

class GraphAttentionLayer(tf.keras.layers.Layer):
    '''
    Single head attention GAT
    Callable instance of class

    Parameters
    ----------
    input_dim: int. the number of feature space of given X
    output_dim: int. the number of expected feature space
    head_num: int. (defaualt 1)

    Output
    ------
    tf.Tensor (N, output_dim)
    '''
    def __init__(self, input_dim, output_dim, head_num=1):
        super(GraphAttentionLayer, self).__init__()
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.head_num = head_num

    def build(self, input_shape):
        '''

        Parameters
        ----------
        input: h = (N, F)
        output: h' = (N, F')
        Returns
        -------

        '''
        # parameterized by a weight matrix W (F', F)
        self.kernel = self.add_weight(shape=(input_shape[-1], self.output_dim), name='W')  # W:(F, F')

        # Parameterized by a weight vector a (2F')
        self.a = self.add_weight(shape=(2*self.output_dim, 1), name='a')
        self.built = True

    def call(self, X):
        # Eqation 1) mapping F feature space to F' features space
        features_i = tf.einsum('ij,jk->ik', X, self.kernel)  # (NxF) (FxF') => WH_i (NxF')
        features_j = tf.einsum('ij,jk->ik', X, self.kernel)  # (NxF) (FxF') => WH_j (NxF')

        # Equation 3) Attention coefficient
        e_ij = tf.tensordot(tf.concat([features_i, features_j], axis=1), self.a, axes=1)
        a_ij = tf.nn.softmax(e_ij, axis=0)  # (N,1)

        # Equation 4) Applying non-linearity with sigma
        context_vec = tf.einsum('ij,ik->ik', a_ij, features_i)  # (N,1) (NxF')
        h = tf.nn.sigmoid(context_vec, name='attention_coefficient')

        return h

모델성능: 성능은 Transductive, inductive 두 가지 방법으로 설명함. (Transductive, inductive을 모른다면, 다음의 포스팅을 클릭). 1) Transductive dataset은 Cora, Citeseer, Pubmed라는 논문 인용에 관한 데이터. Node: 논문, edge: 인용. Node feature: Bag of words in document. Node label: class label.  2) Inductive learning: PPI(단백질-단백질-교호작용) 데이터세트. 그레프 분류

텐서플로2.0 으로 구현한 소스코드와 설명은 다음을 참조

- Github: https://github.com/4pygmalion/GAT_tensorflow

사용이유: 훈련시에 internal covariate shift

훈련모드: 레이어가 미니배치 단위로 mean, std을 현재 미니배치단위마다 얻어와 각 채널별로 정규화해준다.

추론모드: 추론모드는 2가지 방법으로 사용될 수 있다. 

• model.evaluate() 또는 prdict
• layer, model이 training=False인 경우

추론모드에서는 각 훈련모드에서 얻어진 평균과 std을 moving averrage하여 번환한다.

• moving_mean = moving_mean * momentum + mean(batch) * (1 - momentum)
• moving_var = moving_var * momentum + var(batch) * (1 - momentum)

ma * (batch - self.moving_mean) / sqrt(self.moving_var + epsilon) + beta.

따라서, 추론모드는 이미 훈련모드에서 훈련된 상황에서만 사용할 수 있고, 훈련데이터가 추론데이터가 유사한 상황에서 사용될 수 있다. 따라서, 훈련모드와 추론모드에서 둘다 BN(Batch normalization)이 시행된다.

self.moving_mean_initializer = initializers.get(moving_mean_initializer)
self.moving_variance_initializer = initializers.get(moving_variance_initializer)


self.moving_mean = self.add_weight(
          name='moving_mean',
          shape=param_shape,
          dtype=self._param_dtype,
          initializer=self.moving_mean_initializer,
          synchronization=tf_variables.VariableSynchronization.ON_READ,
          trainable=False,
          aggregation=tf_variables.VariableAggregation.MEAN,
          experimental_autocast=False)


self.moving_variance = self.add_weight(
          name='moving_variance',
          shape=param_shape,
          dtype=self._param_dtype,
          initializer=self.moving_variance_initializer,
          synchronization=tf_variables.VariableSynchronization.ON_READ,
          trainable=False,
          aggregation=tf_variables.VariableAggregation.MEAN,
          experimental_autocast=False)
          
          
output, mean, variance = control_flow_util.smart_cond(training, train_op, _fused_batch_norm_inference)
 def mean_update():
   """Update self.moving_mean with the most recent data point."""
   
   if use_fused_avg_updates:
  		return self._assign_new_value(self.moving_mean, mean)
   else:
   		return self._assign_moving_average(self.moving_mean, mean, momentum,
   input_batch_size)

reference: https://keras.io/api/layers/normalization_layers/batch_normalization/