matrix factorization 하면 되는거 아님?
기존 방법론에는 SVD, BCD 등의 방법론이 있습니다.
- SVD 의 문제점: 벡터의 방향을 고유벡터의 5%, 95%값 사이의 있는 벡터를 고름에따라서 이미지 간의 컬러분포(inter-image variation)에 좀 강건하다고는 합니다. 하지만, 전문가가 타깃이미지를 따로 정해주는것대비 별로 성능이 좋지 않다고합니다. 그리고, 고유벡터들이 음의값을 가지거나, 희소성을 보장하지 못하는 경우가 있어서 사용하긴 어렵습니다. 희소성을 가져야하는 이유는 염색이 된 밀도가 각각의 픽셀에서 균등하게 흩어져있으면, 물체(조직)의 구분이 뚜렷하지 않기에 희소성을 갖도록합니다. + 음의 값이 나오면 해석이 어렵습니다. stain density값이 (-)의면 빛이 발산한다는 것이기 때문입니다.
- BCD(Blind color decomposition): 다른 방법론 대비 RMSE가 낮은 matrix factorization이지만 최적화할때 쓰이는 하이퍼파라미터 선정이 매우 까다로워 사용하기 곤란합니다.
SPCN의 주요가정: Non-negativity, sparsity
- Non-negativitiy: 현미경으로 볼때, 조직내에서 빛을 발산하는게 아니라, 흡수만하기 때문에 positive density을 가집니다. 0이면 받은 빛을 모두 투과시키는 것이고, positive이면 조직이 있어서 일부만 흡수되는 것입니다.
- Sparsity: 각 픽셀은 조직의 일부를 표현하고있고, 그 조직은 하나 이상의 염색을 가지고 있다는 것입니다. 예를 들어, 핵 부분은 Hematoxylin에 염색이 주로되고, Eosin에는 소량만 된다는 것입니다. (H와 E에 배타적으로 염색되는 것이 아닙니다). 즉 H&E 각 고유염색의 혼합으로 표현이 가능하다는 것입니다.
- Soft classification: 조직과 조직사이의 가장자리(엣지)의 일부는 2개 이상의 염색이 되어있을 것이다라고 가정
SPCN 방법론
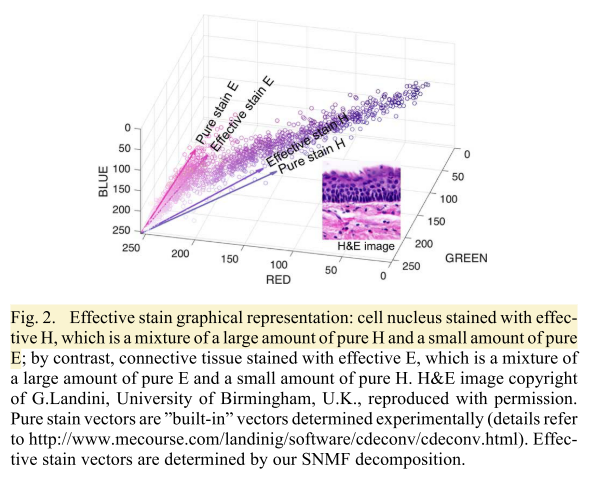
H&E slide을 V를 광학밀도(optical density)로 표현된 이미지로 표현할 수 있습니다. 각 픽셀값을 $V=log\frac{I_{0}}{I}$으로 변경할 수 있습니다. 즉 최대값대비(I0=255, 8bit image) 얼마나 조직에서 흡수되고, 통과된빛이 센서에 남느냐에 대한 지표입니다. 이 V값은 사실, 염색약과 조직이 흡수한정도의 곱으로 표현할 수 있습니다. 그렇기에 아래와 같이 표현이 가능합니다.

$V=WH$
- W은 staining estimation (stain vector)로 염색약의 고유색(color appearance라고도 함)을 의미합니다. m, r 형태며, 컬럼벡터가 염색의 basis(R,G,B 고유색상)이며, r은 염색수를 의미합니다. H&E염색이면 2에 해당됩니다.
- H은 조직이 흡수한 정도를 의미합니다(Stain density).
1. 염색 분리(Stain separation, SNMF-based Stain separation): vahadane의 방식은 V을 W,H로 분해하는 것으로 시작합니다. 아래 목적함수를 만족하려면, W, H가 잘분해되어 V와 같아지면되는데, 이 최적화가 non-convex이기에 global optimum을 만족할 수 없을 수 있습니다(=stain vector(W)추정이 안될수있음).
$min_{W,H} \frac{1}{2}||V-WH||_{F}^{2}$, such that W, H >= 0
W, H가 항상 양수이여이하기때문에 NMF(Non-negative matrix factoriziation)을진행하는데, vahadane은 좀더 진보된 NMF을 제안합니다. W, H가 양수여야하는 이유는 염색자체가 빛을 방출하지는 않고, 흡수만 되기 때문에 그렇습니다.
$min_{W,H} \frac{1}{2}||V-WH||_{F}^{2} + \lambda \sum_{j=1}^{r}||H(j,:)||_{1}$, such that W, H >= 0, $||W(:, j)||^{2}_{2}=1$ (5)
이 식을 표현해보면, 아래와 같습니다.
- $||W(:, j)||^{2}_{2}=1$ : 각 염색별로 고유색상의 R,G,B 흡수욜은 1이 되어야함
- $ \sum_{j=1}^{r}||H(j,:)||_{1}$: 염색별로의 편차가 작아져야함.

근데, 위 5번식을 바로 못풉니다. 그렇기에, W또는 H을 하나 랜덤으로 초기화 후에 고정해놓고, 최적화 합니다. 예를 들어, V은 주어진거니까, W을 고정하고 H을 최적화합니다. 또 한편으로는 H을 고정하고, W을 최적화합니다. 최적화 방법은 sparse coding/dictionary learning 라는 방법으로 최적화합니다.
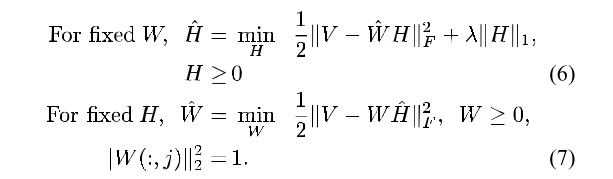
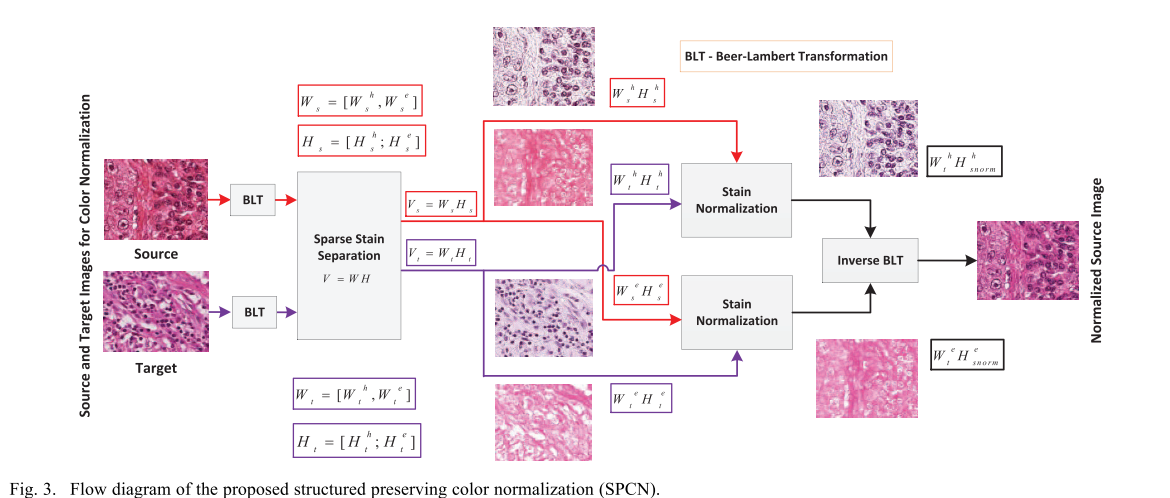
2. Structure-preserving color normalization (SPCN)
1의 stain separation 방법을 적용하면, 금방 stain vectors(matrix, W)와 densitiy(H)을 구할 수 있습니다. 이 방법을 이용해서 다음과 같이 진행합니다.
- Source image s 에 대해서 $W_{s}, H_{s}$을 구합니다.
- target image t 에 대해서 $W_{t}, H_{t}$을 구합니다.
- source image s -> t로 변환하는 작업: 소스 이미지의 염색밀도(stain density, $H_{s}$)에 target image의 염색을 곱해줍니다. $W_{t}H_{s}$ (이 작업으로 염색밀도의 구조적인 내용이 보존된다고하고, 단지W염색만 변경됩니다)
Macenko (PCA based) stain normalization 차이
Macenko et al 의 방식은 염색의 sparseness와 non-negativity을 가정하지 않았기 때문에, 정규화 후에 구조적 정보가 회손될 수 있다고 합니다.
Structure preserving 이라고 하는 이유
이 방법론은 소스 이미지의 염색벡터랑 염색밀도를 각각 구한 다음, "타깃 이미지의 염색벡터"와 "소스 이미지의 염색밀도"를 곱하는 연연산이기 때문에, 염색 밀도는 변하지않고 염색의 색감만 변하게 됩니다. 즉 염색밀도측면에서는 구조적정보가 보존이 됩니다.